Observability of fidelity decay at the Lyapunov rate in few-qubit quantum simulations
Fusion Energy Sciences Program, Lawrence Livermore National Laboratory
| Published: | 2022-09-08, volume 6, page 799 |
| Eprint: | arXiv:2110.07767v2 |
| Doi: | https://doi.org/10.22331/q-2022-09-08-799 |
| Citation: | Quantum 6, 799 (2022). |
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
In certain regimes, the fidelity of quantum states will decay at a rate set by the classical Lyapunov exponent. This serves both as one of the most important examples of the quantum-classical correspondence principle and as an accurate test for the presence of chaos. While detecting this phenomenon is one of the first useful calculations that noisy quantum computers without error correction can perform [G. Benenti et al., Phys. Rev. E 65, 066205 (2001)], a thorough study of the quantum sawtooth map reveals that observing the Lyapunov regime is just beyond the reach of present-day devices. We prove that there are three bounds on the ability of any device to observe the Lyapunov regime and give the first quantitatively accurate description of these bounds: (1) the Fermi golden rule decay rate must be larger than the Lyapunov rate, (2) the quantum dynamics must be diffusive rather than localized, and (3) the initial decay rate must be slow enough for Lyapunov decay to be observable. This last bound, which has not been recognized previously, places a limit on the maximum amount of noise that can be tolerated. The theory implies that an absolute minimum of 6 qubits is required. Recent experiments on IBM-Q and IonQ imply that some combination of a noise reduction by up to 100$\times$ per gate and large increases in connectivity and gate parallelization are also necessary. Finally, scaling arguments are given that quantify the ability of future devices to observe the Lyapunov regime based on trade-offs between hardware architecture and performance.
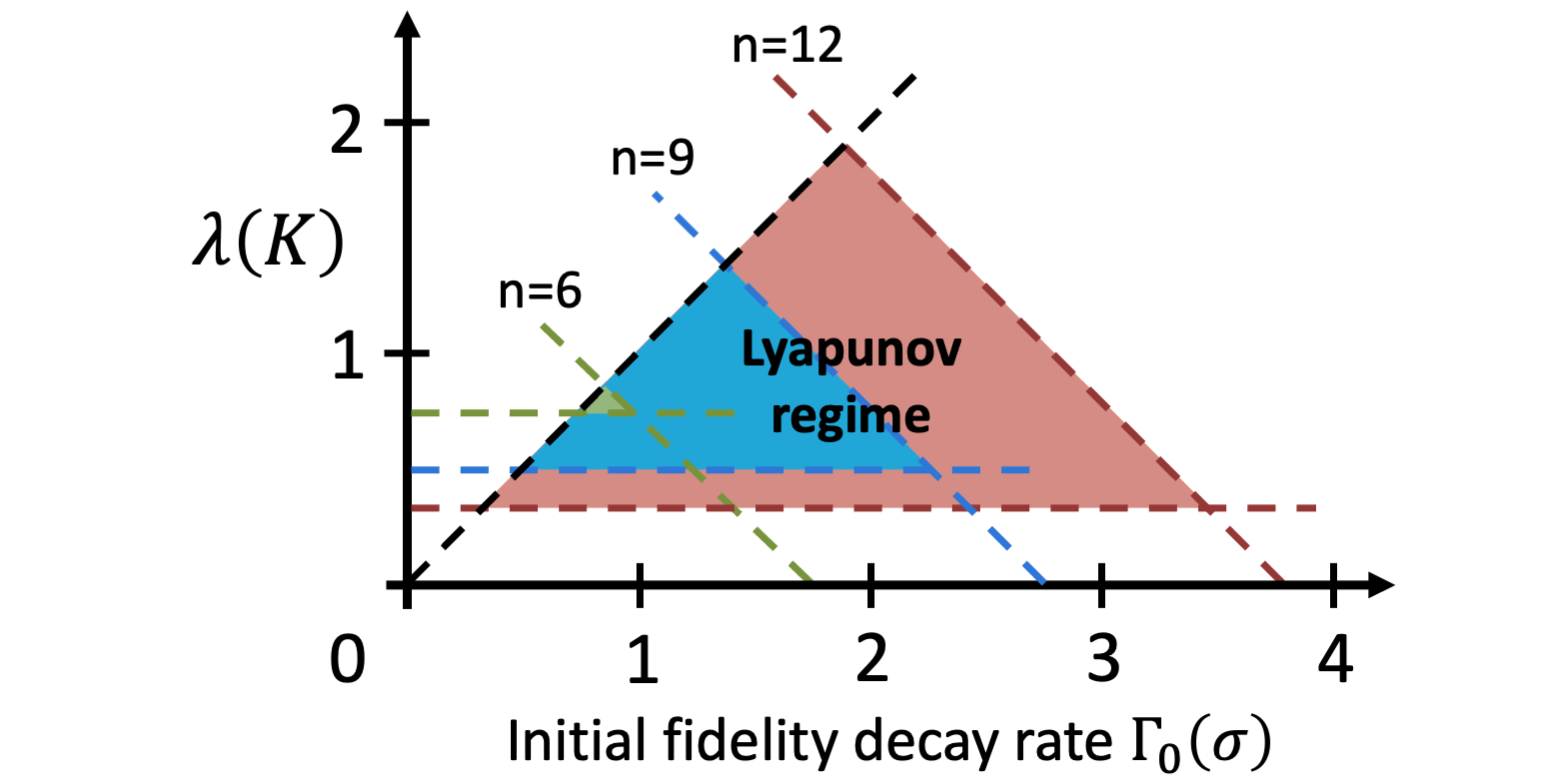
Featured image: The regions of parameter space where the fidelity of a noisy quantum simulation of chaotic dynamics might decay at the Lyapunov rate, for various numbers of qubits $n$. Parameters are the initial fidelity decay rate $\Gamma_0$ and the Lyapunov exponent $\lambda$ of the quantum sawtooth map.
Popular summary
► BibTeX data
► References
[1] Alicia B Magann, Matthew D Grace, Herschel A Rabitz, and Mohan Sarovar. Digital quantum simulation of molecular dynamics and control. Physical Review Research, 3(2):023165, 2021. doi:10.1103/PhysRevResearch.3.023165.
https://doi.org/10.1103/PhysRevResearch.3.023165
[2] Frank Gaitan. Finding flows of a Navier–Stokes fluid through quantum computing. npj Quantum Information, 6(1):1–6, 2020. doi:10.1038/s41534-020-00291-0.
https://doi.org/10.1038/s41534-020-00291-0
[3] Frank Gaitan. Finding solutions of the Navier-Stokes equations through quantum computing—recent progress, a generalization, and next steps forward. Advanced Quantum Technologies, 4(10):2100055, 2021. doi:10.1002/qute.202100055.
https://doi.org/10.1002/qute.202100055
[4] Ilya Y Dodin and Edward A Startsev. On applications of quantum computing to plasma simulations. arXiv preprint arXiv:2005.14369, 2020. doi:10.1063/5.0056974.
https://doi.org/10.1063/5.0056974
arXiv:2005.14369
[5] Yuan Shi, Alessandro R Castelli, Xian Wu, Ilon Joseph, Vasily Geyko, Frank R Graziani, Stephen B Libby, Jeffrey B Parker, Yaniv J Rosen, Luis A Martinez, et al. Simulating non-native cubic interactions on noisy quantum machines. Physical Review A, 103(6):062608, 2021. doi:10.1103/PhysRevA.103.062608.
https://doi.org/10.1103/PhysRevA.103.062608
[6] Karyn Le Hur, Loïc Henriet, Alexandru Petrescu, Kirill Plekhanov, Guillaume Roux, and Marco Schiró. Many-body quantum electrodynamics networks: Non-equilibrium condensed matter physics with light. Comptes Rendus Physique, 17(8):808–835, 2016. doi:10.1016/j.crhy.2016.05.003.
https://doi.org/10.1016/j.crhy.2016.05.003
[7] Sam McArdle, Suguru Endo, Alán Aspuru-Guzik, Simon C Benjamin, and Xiao Yuan. Quantum computational chemistry. Reviews of Modern Physics, 92(1):015003, 2020. doi:10.1103/RevModPhys.92.015003.
https://doi.org/10.1103/RevModPhys.92.015003
[8] Wibe A de Jong, Mekena Metcalf, James Mulligan, Mateusz Płoskoń, Felix Ringer, and Xiaojun Yao. Quantum simulation of open quantum systems in heavy-ion collisions. Physical Review D, 104(5):L051501, 2021. doi:10.1103/PhysRevD.104.L051501.
https://doi.org/10.1103/PhysRevD.104.L051501
[9] Eric T Holland, Kyle A Wendt, Konstantinos Kravvaris, Xian Wu, W Erich Ormand, Jonathan L DuBois, Sofia Quaglioni, and Francesco Pederiva. Optimal control for the quantum simulation of nuclear dynamics. Physical Review A, 101(6):062307, 2020. doi:10.1103/PhysRevA.101.062307.
https://doi.org/10.1103/PhysRevA.101.062307
[10] Esteban A Martinez, Christine A Muschik, Philipp Schindler, Daniel Nigg, Alexander Erhard, Markus Heyl, Philipp Hauke, Marcello Dalmonte, Thomas Monz, Peter Zoller, et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature, 534(7608):516–519, 2016. doi:10.1038/nature18318.
https://doi.org/10.1038/nature18318
[11] Ashley Montanaro. Quantum algorithms: an overview. npj Quantum Information, 2(1):1–8, 2016. doi:10.1038/npjqi.2015.23.
https://doi.org/10.1038/npjqi.2015.23
[12] Andrew M Childs and Wim Van Dam. Quantum algorithms for algebraic problems. Reviews of Modern Physics, 82(1):1, 2010. doi:10.1103/RevModPhys.82.1.
https://doi.org/10.1103/RevModPhys.82.1
[13] Ashley Montanaro. Quantum speedup of monte carlo methods. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 471(2181):20150301, 2015. doi:10.1098/rspa.2015.0301.
https://doi.org/10.1098/rspa.2015.0301
[14] Jules Tilly, Hongxiang Chen, Shuxiang Cao, Dario Picozzi, Kanav Setia, Ying Li, Edward Grant, Leonard Wossnig, Ivan Rungger, George H Booth, et al. The variational quantum eigensolver: a review of methods and best practices. arXiv preprint arXiv:2111.05176, 2021. doi:10.48550/arXiv.2111.05176.
https://doi.org/10.48550/arXiv.2111.05176
arXiv:2111.05176
[15] Sergio Boixo, Sergei V Isakov, Vadim N Smelyanskiy, Ryan Babbush, Nan Ding, Zhang Jiang, Michael J Bremner, John M Martinis, and Hartmut Neven. Characterizing quantum supremacy in near-term devices. Nature Physics, 14(6):595–600, 2018. doi:10.1038/s41567-018-0124-x.
https://doi.org/10.1038/s41567-018-0124-x
[16] Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C Bardin, Rami Barends, Rupak Biswas, Sergio Boixo, Fernando GSL Brandao, David A Buell, et al. Quantum supremacy using a programmable superconducting processor. Nature, 574(7779):505–510, 2019. doi:10.1038/s41586-019-1666-5.
https://doi.org/10.1038/s41586-019-1666-5
[17] Ryan Babbush. Google quantum summer symposium 2021: Google's perspective on the viable applications of early fault-tolerant quantum computers. https://www.youtube.com/watch?v=-fcQt5C2XGY&list=PLpO2pyKisOjL7JdCjzMeOY1w3TnwTkBT-&index=16, 2021. Accessed: 2021-09-27.
https://www.youtube.com/watch?v=-fcQt5C2XGY&list=PLpO2pyKisOjL7JdCjzMeOY1w3TnwTkBT-&index=16
[18] Richard P Feynman. Simulating physics with computers. International Journal of Theoretical Physics, 21(6/7), 1982. doi:10.1201/9780429500459.
https://doi.org/10.1201/9780429500459
[19] Yuri Manin. Computable and uncomputable. Sovetskoye Radio, Moscow, 128, 1980.
[20] Seth Lloyd. Universal quantum simulators. Science, 273(5278):1073–1078, 1996. doi:10.1126/science.273.5278.1073.
https://doi.org/10.1126/science.273.5278.1073
[21] Giuliano Benenti, Giulio Casati, Simone Montangero, and Dima L Shepelyansky. Efficient quantum computing of complex dynamics. Physical Review Letters, 87(22):227901, 2001. doi:10.1103/PhysRevLett.87.227901.
https://doi.org/10.1103/PhysRevLett.87.227901
[22] Giuliano Benenti, Giulio Casati, and Simone Montangero. Quantum computing and information extraction for dynamical quantum systems. Quantum Information Processing, 3(1):273–293, 2004. doi:10.1007/s11128-004-0415-2.
https://doi.org/10.1007/s11128-004-0415-2
[23] Ilon Joseph. Koopman–von Neumann approach to quantum simulation of nonlinear classical dynamics. Physical Review Research, 2(4):043102, 2020. doi:10.1103/PhysRevResearch.2.043102.
https://doi.org/10.1103/PhysRevResearch.2.043102
[24] Jin-Peng Liu, Herman Øie Kolden, Hari K Krovi, Nuno F Loureiro, Konstantina Trivisa, and Andrew M Childs. Efficient quantum algorithm for dissipative nonlinear differential equations. arXiv preprint arXiv:2011.03185, 2020. doi:10.1073/pnas.2026805118.
https://doi.org/10.1073/pnas.2026805118
arXiv:2011.03185
[25] Seth Lloyd, Giacomo De Palma, Can Gokler, Bobak Kiani, Zi-Wen Liu, Milad Marvian, Felix Tennie, and Tim Palmer. Quantum algorithm for nonlinear differential equations. arXiv preprint arXiv:2011.06571, 2020. doi:10.48550/arXiv.2011.06571.
https://doi.org/10.48550/arXiv.2011.06571
arXiv:2011.06571
[26] Alexander Engel, Graeme Smith, and Scott E Parker. Linear embedding of nonlinear dynamical systems and prospects for efficient quantum algorithms. Physics of Plasmas, 28(6):062305, 2021. doi:10.1063/5.0040313.
https://doi.org/10.1063/5.0040313
[27] IY Dodin and EA Startsev. Quantum computation of nonlinear maps. arXiv preprint arXiv:2105.07317, 2021. doi:10.48550/arXiv.2105.07317.
https://doi.org/10.48550/arXiv.2105.07317
arXiv:2105.07317
[28] Aram W Harrow, Avinatan Hassidim, and Seth Lloyd. Quantum algorithm for linear systems of equations. Physical Review Letters, 103(15):150502, 2009. doi:10.1103/PhysRevLett.103.150502.
https://doi.org/10.1103/PhysRevLett.103.150502
[29] Andrew M Childs, Robin Kothari, and Rolando D Somma. Quantum algorithm for systems of linear equations with exponentially improved dependence on precision. SIAM Journal on Computing, 46(6):1920–1950, 2017. doi:10.1137/16M1087072.
https://doi.org/10.1137/16M1087072
[30] Simone Notarnicola, Alessandro Silva, Rosario Fazio, and Angelo Russomanno. Slow heating in a quantum coupled kicked rotors system. Journal of Statistical Mechanics: Theory and Experiment, 2020(2):024008, 2020. doi:10.1088/1742-5468/ab6de4.
https://doi.org/10.1088/1742-5468/ab6de4
[31] Bertrand Georgeot and Dima L Shepelyansky. Exponential gain in quantum computing of quantum chaos and localization. Physical Review Letters, 86(13):2890, 2001. doi:10.1103/PhysRevLett.86.2890.
https://doi.org/10.1103/PhysRevLett.86.2890
[32] Benjamin Lévi and Bertrand Georgeot. Quantum computation of a complex system: The kicked harper model. Physical Review E, 70(5):056218, 2004. doi:doi.org/10.1103/PhysRevE.70.056218.
https://doi.org/10.1103/PhysRevE.70.056218
[33] Klaus M Frahm, Robert Fleckinger, and Dima L Shepelyansky. Quantum chaos and random matrix theory for fidelity decay in quantum computations with static imperfections. The European Physical Journal D-Atomic, Molecular, Optical and Plasma Physics, 29(1):139–155, 2004. doi:10.1140/epjd/e2004-00038-x.
https://doi.org/10.1140/epjd/e2004-00038-x
[34] Rüdiger Schack. Using a quantum computer to investigate quantum chaos. Physical Review A, 57(3):1634, 1998. doi:10.1103/PhysRevA.57.1634.
https://doi.org/10.1103/PhysRevA.57.1634
[35] Giuliano Benenti and Giulio Casati. Quantum-classical correspondence in perturbed chaotic systems. Physical Review E, 65(6):066205, 2002. doi:10.1103/PhysRevE.65.066205.
https://doi.org/10.1103/PhysRevE.65.066205
[36] Giuliano Benenti, Giulio Casati, Simone Montangero, and Dima L Shepelyansky. Dynamical localization simulated on a few-qubit quantum computer. Physical Review A, 67(5):052312, 2003. doi:10.1103/PhysRevA.67.052312.
https://doi.org/10.1103/PhysRevA.67.052312
[37] Wen-ge Wang, Giulio Casati, and Baowen Li. Stability of quantum motion: Beyond fermi-golden-rule and Lyapunov decay. Physical Review E, 69(2):025201, 2004. doi:10.1103/PhysRevE.69.025201.
https://doi.org/10.1103/PhysRevE.69.025201
[38] Andrea Pizzamiglio, Su Yeon Chang, Maria Bondani, Simone Montangero, Dario Gerace, and Giuliano Benenti. Dynamical localization simulated on actual quantum hardware. Entropy, 23(6):654, 2021. doi:10.3390/e23060654.
https://doi.org/10.3390/e23060654
[39] Philippe Jacquod, Peter G Silvestrov, and Carlo WJ Beenakker. Golden rule decay versus Lyapunov decay of the quantum Loschmidt echo. Physical Review E, 64(5):055203, 2001. doi:10.1103/PhysRevE.64.055203.
https://doi.org/10.1103/PhysRevE.64.055203
[40] Philippe Jacquod and Cyril Petitjean. Decoherence, entanglement and irreversibility in quantum dynamical systems with few degrees of freedom. Advances in Physics, 58(2):67–196, 2009. doi:10.1080/00018730902831009.
https://doi.org/10.1080/00018730902831009
[41] Thomas Gorin, Tomaž Prosen, Thomas H Seligman, and Marko Žnidarič. Dynamics of Loschmidt echoes and fidelity decay. Physics Reports, 435(2-5):33–156, 2006. doi:10.1016/j.physrep.2006.09.003.
https://doi.org/10.1016/j.physrep.2006.09.003
[42] Arseni Goussev, Rodolfo A Jalabert, Horacio M Pastawski, and Diego Wisniacki. Loschmidt echo. arXiv preprint arXiv:1206.6348, 2012. doi:10.48550/arXiv.1206.6348.
https://doi.org/10.48550/arXiv.1206.6348
arXiv:1206.6348
[43] Bruno Eckhardt. Echoes in classical dynamical systems. Journal of Physics A: Mathematical and General, 36(2):371, 2002. doi:10.1088/0305-4470/36/2/306.
https://doi.org/10.1088/0305-4470/36/2/306
[44] Asher Peres. Stability of quantum motion in chaotic and regular systems. Physical Review A, 30(4):1610, 1984. doi:10.1103/PhysRevA.30.1610.
https://doi.org/10.1103/PhysRevA.30.1610
[45] Rodolfo A Jalabert and Horacio M Pastawski. Environment-independent decoherence rate in classically chaotic systems. Physical Review Letters, 86(12):2490, 2001. doi:10.1103/PhysRevLett.86.2490.
https://doi.org/10.1103/PhysRevLett.86.2490
[46] Natalia Ares and Diego A Wisniacki. Loschmidt echo and the local density of states. Physical Review E, 80(4):046216, 2009. doi:10.1103/PhysRevE.80.046216.
https://doi.org/10.1103/PhysRevE.80.046216
[47] Ignacio García-Mata and Diego A Wisniacki. Loschmidt echo in quantum maps: the elusive nature of the Lyapunov regime. Journal of Physics A: Mathematical and Theoretical, 44(31):315101, 2011. doi:10.1088/1751-8113/44/31/315101.
https://doi.org/10.1088/1751-8113/44/31/315101
[48] Robert Tyler Sutherland. Private communication, July 2021.
[49] Mohit Pandey, Pieter W Claeys, David K Campbell, Anatoli Polkovnikov, and Dries Sels. Adiabatic eigenstate deformations as a sensitive probe for quantum chaos. Physical Review X, 10(4):041017, 2020. doi:10.1103/PhysRevX.10.041017.
https://doi.org/10.1103/PhysRevX.10.041017
[50] Pedram Roushan et al. Spectroscopic signatures of localization with interacting photons in superconducting qubits. Science, 358(6367):1175–1179, 2017. doi:10.1126/science.aao1401.
https://doi.org/10.1126/science.aao1401
[51] Max D Porter and Ilon Joseph. Impact of dynamics, entanglement, and markovian noise on the fidelity of few-qubit digital quantum simulation. arXiv preprint arXiv:2206.04829, 2022. doi:10.48550/arXiv.2206.04829.
https://doi.org/10.48550/arXiv.2206.04829
arXiv:2206.04829
[52] A Lakshminarayan and NL Balazs. On the quantum cat and sawtooth maps—return to generic behaviour. Chaos, Solitons & Fractals, 5(7):1169–1179, 1995. doi:10.1016/0960-0779(94)E0060-3.
https://doi.org/10.1016/0960-0779(94)E0060-3
[53] Dima Shepelyansky. Ehrenfest time and chaos. Scholarpedia, 15(9):55031, 2020. Accessed: 2022-05-20, doi:10.4249/scholarpedia.55031.
https://doi.org/10.4249/scholarpedia.55031
[54] Jan Šuntajs, Janez Bonča, Tomaž Prosen, and Lev Vidmar. Quantum chaos challenges many-body localization. Physical Review E, 102(6):062144, 2020. doi:10.1103/PhysRevE.102.062144.
https://doi.org/10.1103/PhysRevE.102.062144
[55] Fausto Borgonovi. Localization in discontinuous quantum systems. Physical Review Letters, 80(21):4653, 1998. doi:10.1103/PhysRevLett.80.4653.
https://doi.org/10.1103/PhysRevLett.80.4653
[56] Giulio Casati and Tomaž Prosen. Quantum localization and cantori in the stadium billiard. Physical Review E, 59(3):R2516, 1999. doi:10.1103/PhysRevE.59.R2516.
https://doi.org/10.1103/PhysRevE.59.R2516
[57] RE Prange, R Narevich, and Oleg Zaitsev. Quasiclassical surface of section perturbation theory. Physical Review E, 59(2):1694, 1999. doi:10.1103/PhysRevE.59.1694.
https://doi.org/10.1103/PhysRevE.59.1694
[58] Fernando M Cucchietti, Horacio M Pastawski, and Rodolfo A Jalabert. Universality of the Lyapunov regime for the Loschmidt echo. Physical Review B, 70(3):035311, 2004. doi:10.1103/PhysRevB.70.035311.
https://doi.org/10.1103/PhysRevB.70.035311
[59] Fernando M Cucchietti. The Loschmidt echo in classically chaotic systems: Quantum chaos, irreversibility and decoherence. arXiv preprint quant-ph/0410121, 2004. doi:10.48550/arXiv.quant-ph/0410121.
https://doi.org/10.48550/arXiv.quant-ph/0410121
arXiv:quant-ph/0410121
[60] Thanos Manos and Marko Robnik. Dynamical localization in chaotic systems: Spectral statistics and localization measure in the kicked rotator as a paradigm for time-dependent and time-independent systems. Physical Review E, 87(6):062905, 2013. doi:10.1103/PhysRevE.87.062905.
https://doi.org/10.1103/PhysRevE.87.062905
[61] Vinay Tripathi, Huo Chen, Mostafa Khezri, Ka-Wa Yip, EM Levenson-Falk, and Daniel A Lidar. Suppression of crosstalk in superconducting qubits using dynamical decoupling. arXiv preprint arXiv:2108.04530, 2021. doi:10.48550/arXiv.2108.04530.
https://doi.org/10.48550/arXiv.2108.04530
arXiv:2108.04530
[62] Adi Botea, Akihiro Kishimoto, and Radu Marinescu. On the complexity of quantum circuit compilation. In Eleventh annual symposium on combinatorial search, 2018.
[63] David C McKay, Sarah Sheldon, John A Smolin, Jerry M Chow, and Jay M Gambetta. Three-qubit randomized benchmarking. Physical Review Letters, 122(20):200502, 2019. doi:10.1103/PhysRevLett.122.200502.
https://doi.org/10.1103/PhysRevLett.122.200502
[64] Hardware-aware approach for fault-tolerant quantum computation. https://www.ibm.com/blogs/research/2020/09/hardware-aware-quantum, 2020. Accessed: 2021-11-01.
https://www.ibm.com/blogs/research/2020/09/hardware-aware-quantum
[65] Tanay Roy, Sumeru Hazra, Suman Kundu, Madhavi Chand, Meghan P Patankar, and R Vijay. Programmable superconducting processor with native three-qubit gates. Physical Review Applied, 14(1):014072, 2020. doi:10.1103/PhysRevApplied.14.014072.
https://doi.org/10.1103/PhysRevApplied.14.014072
[66] Brian Marinelli, Jie Luo, Kyunghoon Lee, David Santiago, and Irfan Siddiqi. A dynamically reconfigurable quantum processor architecture. Bulletin of the American Physical Society, 2021. Bibcode:2021APS..MARP32006M.
https://ui.adsabs.harvard.edu/abs/2021APS..MARP32006M
[67] Dmitri Maslov. Basic circuit compilation techniques for an ion-trap quantum machine. New Journal of Physics, 19(2):023035, 2017. doi:10.1088/1367-2630/aa5e47.
https://doi.org/10.1088/1367-2630/aa5e47
[68] Kenneth Wright, Kristin M Beck, et al. Benchmarking an 11-qubit quantum computer. Nature Communications, 10(1):1–6, 2019. doi:10.1038/s41467-019-13534-2.
https://doi.org/10.1038/s41467-019-13534-2
[69] Nikodem Grzesiak et al. Efficient arbitrary simultaneously entangling gates on a trapped-ion quantum computer. Nature Communications, 11(1):1–6, 2020. doi:10.1038/s41467-020-16790-9.
https://doi.org/10.1038/s41467-020-16790-9
[70] David Kielpinski, Chris Monroe, and David J Wineland. Architecture for a large-scale ion-trap quantum computer. Nature, 417(6890):709–711, 2002. doi:10.1038/nature00784.
https://doi.org/10.1038/nature00784
[71] R Tyler Sutherland, Qian Yu, Kristin M Beck, and Hartmut Häffner. One-and two-qubit gate infidelities due to motional errors in trapped ions and electrons. Physical Review A, 105(2):022437, 2022. doi:10.1103/PhysRevA.105.022437.
https://doi.org/10.1103/PhysRevA.105.022437
[72] Kristin M Beck. Private communication, 2021.
[73] Caroline Figgatt, Aaron Ostrander, Norbert M Linke, Kevin A Landsman, Daiwei Zhu, Dmitri Maslov, and Christopher Monroe. Parallel entangling operations on a universal ion-trap quantum computer. Nature, 572(7769):368–372, 2019. doi:10.1038/s41586-019-1427-5.
https://doi.org/10.1038/s41586-019-1427-5
[74] Ming Li, Kenneth Wright, Neal C Pisenti, Kristin M Beck, Jason HV Nguyen, and Yunseong Nam. Generalized hamiltonian to describe imperfections in ion-light interaction. Physical Review A, 102(6):062616, 2020. doi:10.1103/PhysRevA.102.062616.
https://doi.org/10.1103/PhysRevA.102.062616
[75] Daniel Gottesman. The Heisenberg representation of quantum computers. arXiv preprint quant-ph/9807006, 1998. doi:10.48550/arXiv.quant-ph/9807006.
https://doi.org/10.48550/arXiv.quant-ph/9807006
arXiv:quant-ph/9807006
[76] Lorenza Viola, Emanuel Knill, and Seth Lloyd. Dynamical decoupling of open quantum systems. Physical Review Letters, 82(12):2417, 1999. doi:10.1103/PhysRevLett.82.2417.
https://doi.org/10.1103/PhysRevLett.82.2417
[77] Joel J Wallman and Joseph Emerson. Noise tailoring for scalable quantum computation via randomized compiling. Physical Review A, 94(5):052325, 2016. doi:10.1103/PhysRevA.94.052325.
https://doi.org/10.1103/PhysRevA.94.052325
[78] Measurement error mitigation. https://qiskit.org/textbook/ch-quantum-hardware/measurement-error-mitigation.html, 2021. Accessed: 2022-06-20.
https://qiskit.org/textbook/ch-quantum-hardware/measurement-error-mitigation.html
[79] Lorenza Viola and Emanuel Knill. Random decoupling schemes for quantum dynamical control and error suppression. Physical review letters, 94(6):060502, 2005. doi:10.1103/PhysRevLett.94.060502.
https://doi.org/10.1103/PhysRevLett.94.060502
[80] Xian Wu, Spencer L Tomarken, N Anders Petersson, Luis A Martinez, Yaniv J Rosen, and Jonathan L DuBois. High-fidelity software-defined quantum logic on a superconducting qudit. Physical Review Letters, 125(17):170502, 2020. doi:10.1103/PhysRevLett.125.170502.
https://doi.org/10.1103/PhysRevLett.125.170502
[81] Efim B Rozenbaum, Sriram Ganeshan, and Victor Galitski. Lyapunov exponent and out-of-time-ordered correlator’s growth rate in a chaotic system. Physical Review Letters, 118(8):086801, 2017. doi:10.1103/PhysRevLett.118.086801.
https://doi.org/10.1103/PhysRevLett.118.086801
[82] AI Larkin and Yu N Ovchinnikov. Quasiclassical method in the theory of superconductivity. Sov Phys JETP, 28(6):1200–1205, 1969.
[83] Bin Yan, Lukasz Cincio, and Wojciech H Zurek. Information scrambling and Loschmidt echo. Physical Review Letters, 124(16):160603, 2020. doi:10.1103/PhysRevLett.124.160603.
https://doi.org/10.1103/PhysRevLett.124.160603
[84] Sreeram PG, Vaibhav Madhok, and Arul Lakshminarayan. Out-of-time-ordered correlators and the Loschmidt echo in the quantum kicked top: how low can we go? Journal of Physics D: Applied Physics, 54(27):274004, 2021. doi:10.1088/1361-6463/abf8f3.
https://doi.org/10.1088/1361-6463/abf8f3
[85] Jorge Chávez-Carlos, B López-del Carpio, Miguel A Bastarrachea-Magnani, Pavel Stránskỳ, Sergio Lerma-Hernández, Lea F Santos, and Jorge G Hirsch. Quantum and classical Lyapunov exponents in atom-field interaction systems. Physical Review Letters, 122(2):024101, 2019. doi:10.1103/PhysRevLett.122.024101.
https://doi.org/10.1103/PhysRevLett.122.024101
[86] Tomer Goldfriend and Jorge Kurchan. Quasi-integrable systems are slow to thermalize but may be good scramblers. Physical Review E, 102(2):022201, 2020. doi:10.1103/PhysRevE.102.022201.
https://doi.org/10.1103/PhysRevE.102.022201
[87] Atanu Rajak, Roberta Citro, and Emanuele G Dalla Torre. Stability and pre-thermalization in chains of classical kicked rotors. Journal of Physics A: Mathematical and Theoretical, 51(46):465001, 2018. doi:10.1088/1751-8121/aae294.
https://doi.org/10.1088/1751-8121/aae294
[88] Allan J Lichtenberg and Michael A Lieberman. Regular and chaotic dynamics, volume 38. Springer Science & Business Media, 1992.
Cited by
[1] Max D. Porter and Ilon Joseph, "Impact of dynamics, entanglement, and Markovian noise on the fidelity of few-qubit digital quantum simulation", arXiv:2206.04829, (2022).
The above citations are from SAO/NASA ADS (last updated successfully 2024-05-14 21:51:20). The list may be incomplete as not all publishers provide suitable and complete citation data.
Could not fetch Crossref cited-by data during last attempt 2024-05-14 21:51:19: Encountered the unhandled forward link type postedcontent_cite while looking for citations to DOI 10.22331/q-2022-09-08-799.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.