Distinguishing noisy boson sampling from classical simulations
Centro de Ciências Naturais e Humanas, Universidade Federal do ABC, Santo André, SP, 09210-170 Brazil
| Published: | 2021-03-29, volume 5, page 423 |
| Eprint: | arXiv:1905.11458v7 |
| Doi: | https://doi.org/10.22331/q-2021-03-29-423 |
| Citation: | Quantum 5, 423 (2021). |
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
Giving a convincing experimental evidence of the quantum supremacy over classical simulations is a challenging goal. Noise is considered to be the main problem in such a demonstration, hence it is urgent to understand the effect of noise. Recently found classical algorithms can efficiently approximate, to any small error, the output of boson sampling with finite-amplitude noise. In this work it is shown analytically and confirmed by numerical simulations that one can efficiently distinguish the output distribution of such a noisy boson sampling from the approximations accounting for low-order quantum multiboson interferences, what includes the mentioned classical algorithms. The number of samples required to tell apart the quantum and classical output distributions is strongly affected by the previously unexplored parameter: density of bosons, i.e., the ratio of total number of interfering bosons to number of input ports of interferometer. Such critical dependence is strikingly reminiscent of the quantum-to-classical transition in systems of identical particles, which sets in when the system size scales up while density of particles vanishes.
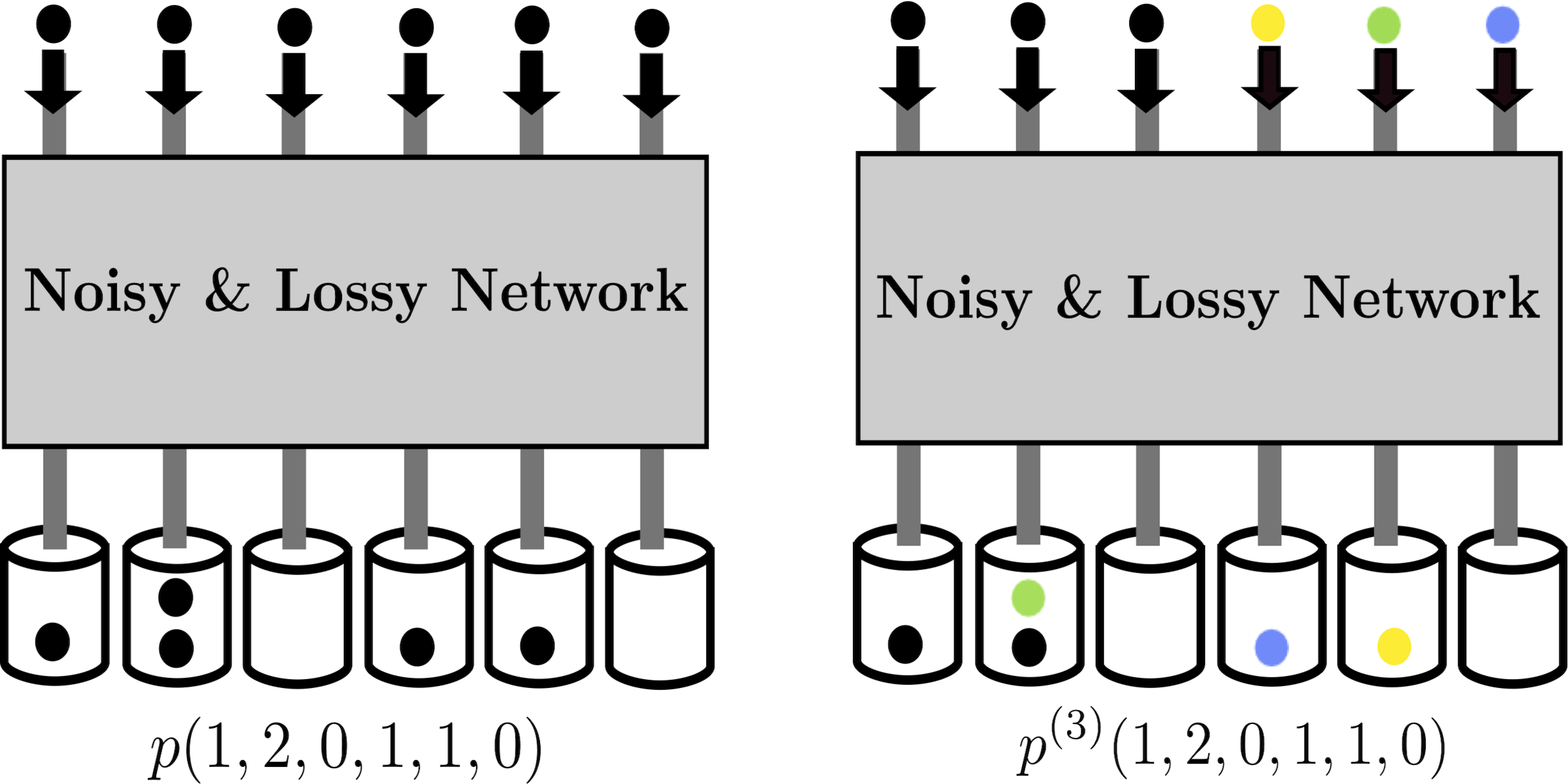
Featured image: Noisy 6-boson sampling (left) vs. classical approximation by a combination of 3-boson interference and 3 distinguishable bosons (right).
Popular summary
► BibTeX data
► References
[1] R. Feynman. Simulating Physics with Computers. Int. J. Theoret. Phys. 21, 467-488 (1982).
https://doi.org/10.1007/BF02650179
[2] P. W. Shor. Algorithms for quantum computation: discrete logarithms and factoring. Proceedings of the 35th Annual Symposium Foundations of Computer Science (IEEE, New York, 1994), p. 124–134.
https://doi.org/10.1109/SFCS.1994.365700
[3] J. Preskill. Quantum Computing in the NISQ era and beyond. Quantum 2, 79 (2018).
https://doi.org/10.22331/q-2018-08-06-79
[4] S. Aaronson and A. Arkhipov, The computational complexity of linear optics. Theory of Computing 9, 143 (2013).
https://doi.org/10.4086/toc.2013.v009a004
[5] M. J. Bremner, A. Montanaro, and D. J. Shepherd. Achieving quantum supremacy with sparse and noisy commuting quantum computations. Quantum 1, 8 (2017).
https://doi.org/10.22331/q-2017-04-25-8
[6] J. Bermejo-Vega, D. Hangleiter, M. Schwarz, R. Raussendorf, and J. Eisert. Architectures for Quantum Simulation Showing a Quantum Speedup. Phys. Rev. X 8, 021010 (2018).
https://doi.org/10.1103/PhysRevX.8.021010
[7] S. O. Boixo, S. V. Isakov, V. N. Smelyanskiy, R. Babbush, N. Ding, Z. Jiang, M. J. Bremner, J. M. Martinis, and H. Neven. Characterizing quantum supremacy in near-term devices. Nature Physics, 14, 595-600 (2018).
https://doi.org/10.1038/s41567-018-0124-x
[8] X. Gao, S.-T. Wang, and L.-M. Duan. Quantum Supremacy for Simulating a Translation-Invariant Ising Spin Model. Phys. Rev. Lett. 118, 040502 (2017).
https://doi.org/10.1103/PhysRevLett.118.040502
[9] F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505-510 (2019).
https://doi.org/10.1038/s41586-019-1666-5
[10] G. Kalai. The Quantum Computer Puzzle. Notices of the AMS, 63, 508-516 (2016).
https://doi.org/10.1090/noti1380
[11] A. Arkhipov and G. Kuperberg. The bosonic birthday paradox. Geometry & Topology Monographs 18, 1-7 (2012).
https://doi.org/10.2140/gtm.2012.18.1
[12] E. R. Caianiello. On quantum field theory — I: explicit solution of Dyson’s equation in electrodynamics without use of Feynman graphs. Nuovo Cimento, 10, 1634-1652 (1953); Combinatorics and Renormalization in Quantum Field Theory, Frontiers in Physics, Lecture Note Series (W. A. Benjamin, Reading, MA, 1973).
https://doi.org/10.1007/BF02781659
[13] S. Scheel. Permanents in linear optical networks. arXiv:quant-ph/0406127.
arXiv:quant-ph/0406127
[14] L. G. Valiant. The complexity of computing the permanent. Theoretical Comput. Sci., 8, 189-201 (1979).
https://doi.org/10.1016/0304-3975(79)90044-6
[15] M. Jerrum, A. Sinclair, and E. Vigoda. A polynomial-time approximation algorithm for the permanent of a matrix with nonnegative entries. Journal of the ACM 51, 671-697 (2004).
https://doi.org/10.1145/1008731.1008738
[16] S. Aaronson. A linear-optical proof that the permanent is $\#$P-hard. Proc. Roy. Soc. London A, 467, 3393–3405 (2011).
https://doi.org/10.1098/rspa.2011.0232
[17] H. Ryser, Combinatorial Mathematics (Cams Mathematical Monographs, No. 14; published by The Mathematical Association of America, distributed by John Wiley and Sons, 1963).
[18] M. A. Broome, A. Fedrizzi, S. Rahimi-Keshari, J. Dove, S. Aaronson, T. C. Ralph, and A. G. White. Photonic Boson Sampling in a Tunable Circuit. Science 339, 794-798 (2013).
https://doi.org/10.1126/science.1231440
[19] J. B. Spring, B. J. Metcalf, P. C. Humphreys, W. S. Kolthammer, X.-M. Jin, M. Barbieri, A. Datta, N. Thomas-Peter, N. K. Langford, D. Kundys, J. C. Gates, B. J. Smith, P. G. R. Smith, and I. A. Walmsley. Boson Sampling on a Photonic Chip. Science, 339, 798-801 (2013).
https://doi.org/10.1126/science.1231692
[20] M. Tillmann, B. Dakić, R. Heilmann, S. Nolte, A. Szameit, and P. Walther. Experimental boson sampling. Nature Photonics, 7, 540-544 (2013).
https://doi.org/10.1038/nphoton.2013.102
[21] A. Crespi, R. Osellame, R. Ramponi, D. J. Brod, E. F. Galvão, N. Spagnolo, C. Vitelli, E. Maiorino, P. Mataloni, and F. Sciarrino. Integrated multimode interferometers with arbitrary designs for photonic boson sampling. Nature Photonics, 7, 545-549 (2013).
https://doi.org/10.1038/nphoton.2013.112
[22] J. Carolan, J. D. A. Meinecke, P. J. Shadbolt, N. J. Russell, N. Ismail, K. Wörhoff, T. Rudolph, M. G. Thompson, J. L. O'Brien, J. C. F. Matthews, and A. Laing. On the experimental verification of quantum complexity in linear optics. Nature Photonics, 8, 621-626 (2014).
https://doi.org/10.1038/nphoton.2014.152
[23] A. P. Lund, A. Laing, S. Rahimi-Keshari, T. Rudolph, J. L. O'Brien, and T. C. Ralph. Boson Sampling from a Gaussian State. Phys. Rev. Lett. 113, 100502 (2014).
https://doi.org/10.1103/PhysRevLett.113.100502
[24] M. Bentivegna, N. Spagnolo, C. Vitelli, F. Flamini, N. Viggianiello, L. Latmiral, P. Mataloni, D. J. Brod, E. F. Galvão, A. Crespi, R. Ramponi, R. Osellame, and F. Sciarrino. Experimental scattershot boson sampling. Science Advances 1, e1400255 (2015).
https://doi.org/10.1126/sciadv.1400255
[25] H.-S. Zhong, L.-C. Peng, Y. Li, Y. Hu, W. Li, J. Qin, D. Wu, W. Zhang, H. Li, L. Zhang, Z. Wang et al. Experimental Gaussian Boson sampling. Science Bulletin, 64, 511-515 (2019).
https://doi.org/10.1016/j.scib.2019.04.007
[26] K. R. Motes, A. Gilchrist, J. P. Dowling, and P. P. Rohde. Scalable Boson Sampling with Time-Bin Encoding Using a Loop-Based Architecture. Phys. Rev. Lett. 113, 120501 (2014).
https://doi.org/10.1103/PhysRevLett.113.120501
[27] Y. He, X. Ding, Z. E. Su, H. L. Huang, J. Qin, C. Wang, S. Unsleber, C. Chen, H. Wang, Y. M. He, et al. Time-Bin-Encoded Boson Sampling with a Single-Photon Device. Phys. Rev. Lett. 118, 190501 (2017).
https://doi.org/10.1103/PhysRevLett.118.190501
[28] J. C. Loredo, M. A. Broome, P. Hilaire, O. Gazzano, I. Sagnes, A. Lemaitre, M. P. Almeida, P. Senellart, and A. G. White. Boson Sampling with Single-Photon Fock States from a Bright Solid-State Source. Phys. Rev. Lett. 118, 130503 (2017).
https://doi.org/10.1103/PhysRevLett.118.130503
[29] H. Wang, Y. He, Y.-H. Li, Z.-E. Su, B. Li, H.-L. Huang, X. Ding, M.-C. Chen, C. Liu, J. Qin et al. High-efficiency multiphoton boson sampling. Nature Photonics 11, 361-365 (2017).
https://doi.org/10.1038/nphoton.2017.63
[30] H. Wang, W. Li, X. Jiang, Y. M. He, Y. H. Li, X. Ding, M. C. Chen, J. Qin, C. Z. Peng, C. Schneider et al. Toward Scalable Boson Sampling with Photon Loss. Phys. Rev. Lett. 120, 230502 (2018).
https://doi.org/10.1103/PhysRevLett.120.230502
[31] H.-S. Zhong, Y. Li, W. Li, L.-C. Peng, Z.-E. Su, Y. Hu, Y.-M. He, X. Ding, W. Zhang, H. Li et al. 12-Photon Entanglement and Scalable Scattershot Boson Sampling with Optimal Entangled-Photon Pairs from Parametric Down-Conversion. Phys. Rev. Lett. 121, 250505 (2018).
https://doi.org/10.1103/PhysRevLett.121.250505
[32] H. Wang, J. Qin, X. Ding, M.-C. Chen, S. Chen, X. You, Y.-M. He, X. Jiang, L. You, Z. Wang, C. Schneider, J. J. Renema, S. Höfling, C.-Y. Lu, and J.-W. Pan. Boson Sampling with 20 Input Photons and a 60-Mode Interferometer in a $10^{14}$-Dimensional Hilbert Space. Phys. Rev. Lett. 123, 250503 (2019).
https://doi.org/10.1103/PhysRevLett.123.250503
[33] C. Shen, Z. Zhang, and L.-M. Duan. Scalable Implementation of Boson Sampling with Trapped Ions. Phys. Rev. Lett. 112, 050504 (2014).
https://doi.org/10.1103/PhysRevLett.112.050504
[34] B. Peropadre, G. G. Guerreschi, J. Huh, and A. Aspuru-Guzik. Proposal for Microwave Boson Sampling. Phys. Rev. Lett. 117, 140505 (2016).
https://doi.org/10.1103/PhysRevLett.117.140505
[35] S. Goldstein, S. Korenblit, Y. Bendor, H. You, M. R. Geller, and N. Katz. Decoherence and interferometric sensitivity of boson sampling in superconducting resonator networks. Phys. Rev. B 95, 020502(R) (2017).
https://doi.org/10.1103/PhysRevB.95.020502
[36] A. Deshpande, B. Fefferman, M. C. Tran, M. Foss-Feig and A. V. Gorshkov. Dynamical Phase Transitions in Sampling Complexity. Phys. Rev. Lett. 121, 030501 (2018).
https://doi.org/10.1103/PhysRevLett.121.030501
[37] B. Peropadre, J. Huk and C. Sabín. Dynamical Casimir Effect for Gaussian Boson Sampling. Scientific Reports 8, 3751 (2018).
https://doi.org/10.1038/s41598-018-22086-2
[38] A. Neville, C. Sparrow, R. Clifford, E. Johnston, P. M. Birchall, A. Montanaro, and A. Laing. Classical boson sampling algorithms with superior performance to near-term experiments. Nature Physics 13, 1153-1157 (2017).
https://doi.org/10.1038/nphys4270
[39] P. Clifford, and R. Clifford. The Classical Complexity of Boson Sampling. Proceedings of the 2018 Annual ACM-SIAM Symposium on Discrete Algorithms pp. 146–55.
https://doi.org/10.1137/1.9781611975031.10
[40] G. Kalai and G. Kindler. Gaussian Noise Sensitivity and BosonSampling. arXiv:1409.3093 [quant-ph].
arXiv:1409.3093
[41] A. Leverrier and R. García-Patrón. Analysis of circuit imperfections in BosonSampling. Quant. Inf. & Computation 15, 489-512 (2015).
https://dl.acm.org/doi/abs/10.5555/2871401.2871409
[42] V. S. Shchesnovich. Sufficient condition for the mode mismatch of single photons for scalability of the boson-sampling computer. Phys. Rev. A 89, 022333 (2014).
https://doi.org/10.1103/PhysRevA.89.022333
[43] A. Arkhipov. BosonSampling is robust against small errors in the network matrix. Phys. Rev. A 92, 062326 (2015).
https://doi.org/10.1103/PhysRevA.92.062326
[44] S. Aaronson and D. J. Brod. BosonSampling with lost photons. Phys. Rev. A 93, 012335 (2016).
https://doi.org/10.1103/PhysRevA.93.012335
[45] L. Latmiral, N. Spagnolo and F. Sciarrino. Towards quantum supremacy with lossy scattershot boson sampling. New J. Phys. 18, 113008 (2016).
https://doi.org/10.1088/1367-2630/18/11/113008
[46] P. P. Rohde and T. C. Ralph. Error tolerance of the boson-sampling model for linear optics quantum computing. Phys. Rev. A 85, 022332 (2012).
https://doi.org/10.1103/PhysRevA.85.022332
[47] S. Rahimi-Keshari, T. C. Ralph, and C. M. Caves. Sufficient Conditions for Efficient Classical Simulation of Quantum Optics. Phys. Rev. X 6, 021039 (2016).
https://doi.org/10.1103/PhysRevX.6.021039
[48] J. J. Renema, A. Menssen, W. R. Clements, G. Triginer, W. S. Kolthammer, and I. A. Walmsley. Efficient Classical Algorithm for Boson Sampling with Partially Distinguishable Photons. Phys. Rev. Lett. 120, 220502 (2018).
https://doi.org/10.1103/PhysRevLett.120.220502
[49] M. Oszmaniec and D. J. Brod. Classical simulation of photonic linear optics with lost particles. New J. Phys. 20, 092002 (2018).
https://doi.org/10.1088/1367-2630/aadfa8
[50] R. García-Patrón, J. J. Renema, and V. S. Shchesnovich. Simulating boson sampling in lossy architectures. Quantum 3, 169 (2019).
https://doi.org/10.22331/q-2019-08-05-169
[51] D. J. Brod and M. Oszmaniec. Classical simulation of linear optics subject to nonuniform losses. Quantum 4, 267 (2020).
https://doi.org/10.22331/q-2020-05-14-267
[52] J. J. Renema, V. S. Shchesnovich, and R. García-Patrón. Classical simulability of noisy boson sampling. arXiv:1809.01953 [quant-ph].
arXiv:1809.01953
[53] V. S. Shchesnovich. Noise in boson sampling and the threshold of efficient classical simulatability. Phys. Rev. A 100, 012340 (2019).
https://doi.org/10.1103/PhysRevA.100.012340
[54] S. Aaronson and A. Arkhipov. Bosonsampling is far from uniform. Quant. Inform. & Computation 14, 1383 (2014).
https://dl.acm.org/doi/10.5555/2685179.2685186
[55] C. Gogolin, M. Kliesch, L. Aolita, and J. Eisert. Boson-Sampling in the light of sample complexity. arXiv:1306.3995 [quant-ph].
arXiv:1306.3995
[56] V. S. Shchesnovich. Universality of Generalized Bunching and Efficient Assessment of Boson Sampling. Phys. Rev. Lett. 116, 123601 (2016).
https://doi.org/10.1103/PhysRevLett.116.123601
[57] M. Walschaers, J. Kuipers, J.-D. Urbina, K. Mayer, M. C. Tichy, K. Richter, and A. Buchleitner. Statistical benchmark for BosonSampling. New J. Phys. 18, 032001 (2016).
https://doi.org/10.1088/1367-2630/18/3/032001
[58] T. Giordani, F. Flamini, M. Pompili, N. Viggianiello, N. Spagnolo, A. Crespi, R. Osellame, N. Wiebe, M. Walschaers, A. Buchleitner, and F. Sciarrino. Experimental statistical signature of many-body quantum interference. Nature Photonics 12, 173-178 (2018).
https://doi.org/10.1038/s41566-018-0097-4
[59] S. T. Wang and L.-M. Duan. Certification of Boson Sampling Devices with Coarse-Grained Measurements. arXiv:1601.02627 [quant-ph].
arXiv:1601.02627
[60] I. Agresti, N. Viggianiello, F. Flamini, N. Spagnolo, A. Crespi, R. Osellame, N. Wiebe, and F. Sciarrino. Pattern Recognition Techniques for Boson Sampling Validation. Phys. Rev. X 9, 011013 (2019).
https://doi.org/10.1103/PhysRevX.9.011013
[61] V. S. Shchesnovich. On the classical complexity of sampling from quantum interference of indistinguishable bosons. Int. J. of Quantum Inform. 18, 2050044 (2020).
https://doi.org/10.1142/S0219749920500446
[62] A. I. Barvinok. Two Algorithmic Results for the Traveling Salesman Problem. Math. of Oper. Research, 21 65-84 (1996); see theorem (3.3).
https://doi.org/10.1287/moor.21.1.65
[63] V. S. Shchesnovich. Asymptotic evaluation of bosonic probability amplitudes in linear unitary networks in the case of large number of bosons. Int. J. Quantum Inform. 11, 1350045 (2013); see appendix D.
https://doi.org/10.1142/S0219749913500457
[64] A. E. Moylett, R. García-Patrón, J. J. Renema, and P. S. Turner. Classically simulating near-term partially-distinguishable and lossy boson sampling. Quantum Sci. Technol. 5, 015001 (2020).
https://doi.org/10.1088/2058-9565/ab5555
[65] A. L. Migdall, D. Branning, and S. Castelletto. Tailoring single-photon and multiphoton probabilities of a single-photon on-demand source. Phys. Rev. A 66, 053805. (2002).
https://doi.org/10.1103/PhysRevA.66.053805
[66] S. M. Barnett, C. R. Gilson, B. Huttner, and N. Imoto. Field Commutation Relations in Optical Cavities. Phys. Rev. Lett. 77, 1739 (1996).
https://doi.org/10.1103/PhysRevLett.77.1739
[67] C. K. Hong, Z. Y. Ou, and L. Mandel. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044 (1987).
https://doi.org/10.1103/PhysRevLett.59.2044
[68] V. S. Shchesnovich. Partial indistinguishability theory for multiphoton experiments in multiport devices. Phys. Rev. A 91, 013844 (2015).
https://doi.org/10.1103/PhysRevA.91.013844
[69] R. P. Stanley, Enumerative Combinatorics, 2nd ed., Vol. 1 (Cambridge University Press, 2011).
[70] V. S. Shchesnovich and M. E. O. Bezerra. Collective phases of identical particles interfering on linear multiports. Phys. Rev. A 98, 033805 (2018).
https://doi.org/10.1103/PhysRevA.98.033805
[71] V. S. Shchesnovich and M. E. O. Bezerra. Distinguishability theory for time-resolved photodetection and boson sampling. Phys. Rev. A 101, 053853 (2020).
https://doi.org/10.1103/PhysRevA.101.053853
[72] Z. Puchala and J. A. Miszczak. Symbolic integration with respect to the Haar measure on the unitary groups. Bull. Polish Acad. Sci.: Techn. Sci. 65, 21-27 (2017).
https://doi.org/10.1515/bpasts-2017-0003
[73] V. S. Shchesnovich. Asymptotic Gaussian law for noninteracting indistinguishable particles in random networks. Scientific Reports 7, 31 (2017).
https://doi.org/10.1038/s41598-017-00044-8
[74] S. Rahimi-Keshari, A. P. Lund, and T. C. Ralph. What Can Quantum Optics Say about Computational Complexity Theory? Phys. Rev. Lett. 114, 060501 (2015).
https://doi.org/10.1103/PhysRevLett.114.060501
[75] L. Chakhmakhchyan, N. J. Cerf, and R. García-Patrón. Quantum-inspired algorithm for estimating the permanent of positive semidefinite matrices. Phys. Rev. A 96, 022329 (2017).
https://doi.org/10.1103/PhysRevA.96.022329
[76] A. Agresti and B. A. Coull. Approximate is Better than “Exact” for Interval Estimation of Binomial Proportions. The American Statistician 52, 119-126 (1998).
https://doi.org/10.1080/00031305.1998.10480550
[77] N. N. Bogolyubov and N. N. Bogolyubov (Jr.), Introduction to Quantum Statistical Mechanics (Nauka, Moscow (1984)).
[78] M. N. Anderson, J. R. Ensher, M. R. Mathews, C. E. Wieman and E. A. Cornell. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 269, 198-201 (1995).
https://doi.org/10.1126/science.269.5221.198
[79] K. B. Davis, M.-O. Mewes, M. R. Andrews, N. J. van Druten, D. S. Durfee, D. M. Kurn, and W. Ketterle. Bose-Einstein Condensation in a Gas of Sodium Atoms. Phys. Rev. Lett. 75, 3969 (1995).
https://doi.org/10.1103/PhysRevLett.75.3969
[80] L. P. Pitaevskii. Vortex lines in an imperfect Bose gas. Soviet Phys. JETP 13, 451-454 (1961).
http://jetp.ac.ru/cgi-bin/dn/e_013_02_0451.pdf
[81] E. P. Gross. Structure of a quantized vortex in boson systems. Il Nuovo Cimento 20, 454-477 (1961).
https://doi.org/10.1007/BF02731494
[82] L. Takács. On the Method of Inclusion and Exclusion. J. of Amer. Stat. Assoc. 62, 102-113 (1967).
https://doi.org/10.2307/2282913
Cited by
[1] Benoit Seron and Antoine Restivo, "BosonSampling.jl: A Julia package for quantum multi-photon interferometry", Quantum 8, 1378 (2024).
[2] Valery Shchesnovich, "Distinguishability in quantum interference with multimode squeezed states", Physical Review A 105 6, 063703 (2022).
[3] Aaron W. Young, Shawn Geller, William J. Eckner, Nathan Schine, Scott Glancy, Emanuel Knill, and Adam M. Kaufman, "An atomic boson sampler", Nature 629 8011, 311 (2024).
[4] Nicolas Heurtel, Shane Mansfield, Jean Senellart, and Benoît Valiron, "Strong simulation of linear optical processes", Computer Physics Communications 291, 108848 (2023).
[5] Alexander S. Dellios, Margaret D. Reid, and Peter D. Drummond, "Simulating Gaussian boson sampling quantum computers", AAPPS Bulletin 33 1, 31 (2023).
[6] Dominik Hangleiter and Jens Eisert, "Computational advantage of quantum random sampling", Reviews of Modern Physics 95 3, 035001 (2023).
[7] Yu-Hao Deng, Yi-Chao Gu, Hua-Liang Liu, Si-Qiu Gong, Hao Su, Zhi-Jiong Zhang, Hao-Yang Tang, Meng-Hao Jia, Jia-Min Xu, Ming-Cheng Chen, Jian Qin, Li-Chao Peng, Jiarong Yan, Yi Hu, Jia Huang, Hao Li, Yuxuan Li, Yaojian Chen, Xiao Jiang, Lin Gan, Guangwen Yang, Lixing You, Li Li, Han-Sen Zhong, Hui Wang, Nai-Le Liu, Jelmer J. Renema, Chao-Yang Lu, and Jian-Wei Pan, "Gaussian Boson Sampling with Pseudo-Photon-Number-Resolving Detectors and Quantum Computational Advantage", Physical Review Letters 131 15, 150601 (2023).
[8] Alexandra E. Moylett, "Spot the Difference: Distinguishing Boson Sampling Experiments from Classical Simulations", Quantum Views 5, 53 (2021).
[9] V. S. Shchesnovich, "Noise in boson sampling and the threshold of efficient classical simulatability", Physical Review A 100 1, 012340 (2019).
[10] Jelmer J. Renema, "Marginal probabilities in boson samplers with arbitrary input states", arXiv:2012.14917, (2020).
The above citations are from Crossref's cited-by service (last updated successfully 2024-07-26 13:27:53) and SAO/NASA ADS (last updated successfully 2024-07-26 13:27:54). The list may be incomplete as not all publishers provide suitable and complete citation data.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.
Pingback: Perspective in Quantum Views by Alexandra E. Moylett "Spot the Difference: Distinguishing Boson Sampling Experiments from Classical Simulations"