Relational superposition measurements with a material quantum ruler

Hui Wang; Flaminia Giacomini; Franco Nori; Miles P. Blencowe

doi:10.22331/q-2024-05-06-1335

Relational superposition measurements with a material quantum ruler

Hui Wang^1,2, Flaminia Giacomini^3,4, Franco Nori^2,5,6, and Miles P. Blencowe¹

¹Department of Physics and Astronomy, Dartmouth College, Hanover, New Hampshire 03755, USA
²Theoretical Quantum Physics Laboratory, Cluster for Pioneering Research, RIKEN, Wako-shi, Saitama 351-0198, Japan
³Perimeter Institute for Theoretical Physics, 31 Caroline St. N, Waterloo, Ontario, N2L 2Y5, Canada
⁴Institute for Theoretical Physics, ETH Zürich, Wolfgang-Pauli-Str. 27, Zürich, Switzerland
⁵Quantum Computing Center, RIKEN, Wako-shi, Saitama 351-0198, Japan
⁶Department of Physics, University of Michigan, Ann Arbor, Michigan 48109-1040, USA

Published:	2024-05-06, volume 8, page 1335
Eprint:	arXiv:2306.00347v4
Doi:	https://doi.org/10.22331/q-2024-05-06-1335
Citation:	Quantum 8, 1335 (2024).

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

In physics, it is crucial to identify operational measurement procedures to give physical meaning to abstract quantities. There has been significant effort to define time operationally using quantum systems, but the same has not been achieved for space. Developing an operational procedure to obtain information about the location of a quantum system is particularly important for a theory combining general relativity and quantum theory, which cannot rest on the classical notion of spacetime. Here, we take a first step towards this goal, and introduce a model to describe an extended material quantum system working as a position measurement device. Such a "quantum ruler" is composed of $N$ harmonically interacting dipoles and serves as a (quantum) reference system for the position of another quantum system. We show that we can define a quantum measurement procedure corresponding to the "superposition of positions", and that by performing this measurement we can distinguish when the quantum system is in a coherent or incoherent superposition in the position basis. The model is fully relational, because the only meaningful variables are the relative positions between the ruler and the system, and the measurement is expressed in terms of an interaction between the measurement device and the measured system.

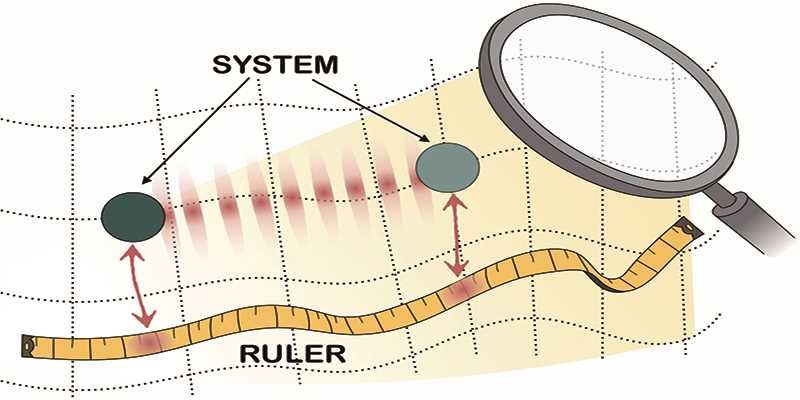
Featured image: Intuitive illustration of the functioning of the quantum ruler. We introduce a relational position measurement scheme for systems in a spatial quantum superposition, which does not depend on any abstract or absolute quantity and is solely expressed in terms of relations between two physical systems. Central to the idea is to develop a concrete model of a quantum ruler which interacts (red arrows) with a quantum system initially prepared in a quantum superposition state of two different locations. The ruler is distorted (red spots) as a result of the interaction with the system. We show that after the measurement, which involves both the ruler and the quantum system, the coherence of the quantum superposition (the interference pattern) can be preserved.

Popular summary

In quantum physics, defining abstract concepts like time and space is not as straightforward as it might seem. A fruitful way to make progress in our understanding of these abstract concepts is to “operationally” construct concrete quantum models involving their measurement. While considerable progress has been made in operationally defining time using quantum clock models, operational definitions of spatial position measurements remain largely unexplored. Developing an operational procedure to obtain information about the evolving location of a quantum system is particularly important in order to further our understanding of the interface between quantum theory and gravity, where classical notions of space and time break down.

Here we propose and develop a concrete model of a “quantum ruler” that crucially meets the challenge of verifying that the ruler-measured particle system behaves according to quantum mechanics. Despite the many technical challenges in developing such a model, we have nevertheless made progress in overcoming some of them. By further refining the quantum ruler model and investigating new scenarios involving dynamical quantum systems, we can extend our findings in several directions, such as constructing more realistic models of the ruler and its interaction with various measured systems, including quantum field systems.

► BibTeX data

@article{Wang2024relational,
  doi = {10.22331/q-2024-05-06-1335},
  url = {https://doi.org/10.22331/q-2024-05-06-1335},
  title = {Relational superposition measurements with a material quantum ruler},
  author = {Wang, Hui and Giacomini, Flaminia and Nori, Franco and Blencowe, Miles P.},
  journal = {{Quantum}},
  issn = {2521-327X},
  publisher = {{Verein zur F{\"{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}},
  volume = {8},
  pages = {1335},
  month = may,
  year = {2024}
}

► References

[1] Asher Peres, Petra F. Scudo, and Daniel R. Terno. ``Quantum entropy and special relativity''. Phys. Rev. Lett. 88, 230402 (2002). arXiv:quant-ph/0203033.
https://doi.org/10.1103/PhysRevLett.88.230402
arXiv:quant-ph/0203033

[2] Heiko Bauke, Sven Ahrens, Christoph H. Keitel, and Rainer Grobe. ``What is the relativistic spin operator?''. New Journal of Physics 16, 043012 (2014). arXiv:1303.3862.
https://doi.org/10.1088/1367-2630/16/4/043012
arXiv:1303.3862

[3] Paul Erker, Mark T Mitchison, Ralph Silva, Mischa P Woods, Nicolas Brunner, and Marcus Huber. ``Autonomous quantum clocks: does thermodynamics limit our ability to measure time?''. Phys. Rev. X 7, 031022 (2017). arXiv:1609.06704.
https://doi.org/10.1103/PhysRevX.7.031022
arXiv:1609.06704

[4] Mischa P Woods, Ralph Silva, Gilles Pütz, Sandra Stupar, and Renato Renner. ``Quantum clocks are more accurate than classical ones''. PRX Quantum 3, 010319 (2022). arXiv:1806.00491.
https://doi.org/10.1103/PRXQuantum.3.010319
arXiv:1806.00491

[5] Guglielmo M. Tino et al. ``Atom interferometers and optical atomic clocks: New quantum sensors for fundamental physics experiments in space''. Nucl. Phys. B Proc. Suppl. 166, 159–165 (2007).
https://doi.org/10.1016/j.nuclphysbps.2006.12.061

[6] Magdalena Zych, Fabio Costa, Igor Pikovski, and Časlav Brukner. ``Quantum interferometric visibility as a witness of general relativistic proper time''. Nature communications 2, 505 (2011). arXiv:1105.4531.
https://doi.org/10.1038/ncomms1498
arXiv:1105.4531

[7] Domenico Giulini. ``Equivalence principle, quantum mechanics, and atom-interferometric tests''. Pages 345–370. Springer Basel. Basel (2012). arXiv:1105.0749.
https://doi.org/10.1007/978-3-0348-0043-3_16
arXiv:1105.0749

[8] Magdalena Zych, Igor Pikovski, Fabio Costa, and Časlav Brukner. ``General relativistic effects in quantum interference of “clocks”''. Journal of Physics: Conference Series 723, 012044 (2016). arXiv:1607.04022.
https://doi.org/10.1088/1742-6596/723/1/012044
arXiv:1607.04022

[9] Albert Roura. ``Gravitational redshift in quantum-clock interferometry''. Phys. Rev. X 10, 021014 (2020). arXiv:1810.06744.
https://doi.org/10.1103/PhysRevX.10.021014
arXiv:1810.06744

[10] Peter Knight. ``Measuring quantum states with quantum rulers''. In International Quantum Electronics Conference. Page FF2. Optica Publishing Group (1996). url: opg.optica.org/abstract.cfm?URI=IQEC-1996-FF2.
https://opg.optica.org/abstract.cfm?URI=IQEC-1996-FF2

[11] Timothy C. Ralph. ``Coherent superposition states as quantum rulers''. Phys. Rev. A 65, 042313 (2002). arXiv:quant-ph/0109106.
https://doi.org/10.1103/PhysRevA.65.042313
arXiv:quant-ph/0109106

[12] Bryce S. DeWitt. ``Quantum theory of gravity. I. The canonical theory''. Phys. Rev. 160, 1113 (1967).
https://doi.org/10.1103/PhysRev.160.1113

[13] Karel V. Kuchar and Charles G. Torre. ``Gaussian reference fluid and interpretation of quantum geometrodynamics''. Phys. Rev. D 43, 419–441 (1991).
https://doi.org/10.1103/PhysRevD.43.419

[14] J. David Brown and Karel V. Kuchar. ``Dust as a standard of space and time in canonical quantum gravity''. Phys. Rev. D 51, 5600–5629 (1995). arXiv:gr-qc/9409001.
https://doi.org/10.1103/PhysRevD.51.5600
arXiv:gr-qc/9409001

[15] J. David Brown and Donald Marolf. ``On relativistic material reference systems''. Phys. Rev. D 53, 1835–1844 (1996). arXiv:gr-qc/9509026.
https://doi.org/10.1103/PhysRevD.53.1835
arXiv:gr-qc/9509026

[16] George F. R. Ellis and Rituparno Goswami. ``Space time and the passage of time''. In Abhay Ashtekar and Vesselin Petkov, editors, Springer Handbook of Spacetime. Pages 243–264. Springer (2014). arXiv:1208.2611.
https://doi.org/10.1007/978-3-642-41992-8_13
arXiv:1208.2611

[17] Carlo Rovelli. ``Quantum gravity''. Cambridge Monographs on Mathematical Physics. Cambridge University Press. (2004).
https://doi.org/10.1017/CBO9780511755804

[18] Carlo Rovelli. ``Relational quantum mechanics''. Int. J. Theor. Phys. 35, 1637–1678 (1996). arXiv:quant-ph/9609002.
https://doi.org/10.1007/BF02302261
arXiv:quant-ph/9609002

[19] Edward Anderson. ``The problem of time''. Springer. (2017).
https://doi.org/10.1007/978-3-319-58848-3

[20] Juan I Cirac and Peter Zoller. ``Quantum computations with cold trapped ions''. Phys. Rev. Lett. 74, 4091–4094 (1995).
https://doi.org/10.1103/PhysRevLett.74.4091

[21] Wentao Chen, Yao Lu, Shuaining Zhang, Kuan Zhang, Guanhao Huang, Mu Qiao, Xiaolu Su, Jialiang Zhang, Jing-Ning Zhang, Leonardo Banchi, M. S. Kim, and Kihwan Kim. ``Scalable and programmable phononic network with trapped ions''. Nat. Phys.Pages 1–7 (2023). arXiv:2207.06115.
https://doi.org/10.1038/s41567-023-01952-5
arXiv:2207.06115

[22] E. Vetsch, D. Reitz, G. Sagué, R. Schmidt, S. T. Dawkins, and A. Rauschenbeutel. ``Optical interface created by laser-cooled atoms trapped in the evanescent field surrounding an optical nanofiber''. Phys. Rev. Lett. 104, 203603 (2010). arXiv:0912.1179.
https://doi.org/10.1103/PhysRevLett.104.203603
arXiv:0912.1179

[23] David Edward Bruschi. ``Time evolution of coupled multimode and multiresonator optomechanical systems''. J. Math. Phys. 60, 062105 (2019). arXiv:1812.06879.
https://doi.org/10.1063/1.5106409
arXiv:1812.06879

[24] Wojciech H. Zurek. ``Decoherence and the Transition from Quantum to Classical''. Physics Today 44, 36–44 (1991).
https://doi.org/10.1063/1.881293

[25] Donald Lynden-Bell and Joseph Katz. ``Classical mechanics without absolute space''. Phys. Rev. D 52, 7322–7324 (1995). arXiv:astro-ph/9509158.
https://doi.org/10.1103/PhysRevD.52.7322
arXiv:astro-ph/9509158

[26] Bianca Dittrich. ``Partial and complete observables for Hamiltonian constrained systems''. Gen. Rel. Grav. 39, 1891–1927 (2007). arXiv:gr-qc/0411013.
https://doi.org/10.1007/s10714-007-0495-2
arXiv:gr-qc/0411013

[27] Johannes Tambornino. ``Relational Observables in Gravity: a Review''. SIGMA 8, 017 (2012). arXiv:1109.0740.
https://doi.org/10.3842/SIGMA.2012.017
arXiv:1109.0740

[28] Philipp A. Hoehn, Alexander R. H. Smith, and Maximilian P. E. Lock. ``Trinity of relational quantum dynamics''. Phys. Rev. D 104, 066001 (2021). arXiv:1912.00033.
https://doi.org/10.1103/PhysRevD.104.066001
arXiv:1912.00033

[29] Kristina Giesel, Bao-Fei Li, and Parampreet Singh. ``Relating dust reference models to conventional systems in manifestly gauge invariant perturbation theory''. Phys. Rev. D 104, 023501 (2021). arXiv:2012.14443.
https://doi.org/10.1103/PhysRevD.104.023501
arXiv:2012.14443

[30] Martin Bojowald, Luiz Martinez, and Garrett Wendel. ``Relational evolution with oscillating clocks''. Phys. Rev. D 105, 106020 (2022). arXiv:2110.07702.
https://doi.org/10.1103/PhysRevD.105.106020
arXiv:2110.07702

[31] Alessio Baldazzi, Kevin Falls, and Renata Ferrero. ``Relational observables in asymptotically safe gravity''. Annals Phys. 440, 168822 (2022). arXiv:2112.02118.
https://doi.org/10.1016/j.aop.2022.168822
arXiv:2112.02118

[32] Johannes Kofler and Časlav Brukner. ``Classical world arising out of quantum physics under the restriction of coarse-grained measurements''. Phys. Rev. Lett. 99, 180403 (2007). arXiv:quant-ph/0609079.
https://doi.org/10.1103/PhysRevLett.99.180403
arXiv:quant-ph/0609079

[33] Borivoje Dakić and Časlav Brukner. ``The Classical Limit of a Physical Theory and the Dimensionality of Space''. Fundam. Theor. Phys. 181, 249–282 (2016). arXiv:1307.3984.
https://doi.org/10.1007/978-94-017-7303-4_8
arXiv:1307.3984

[34] Ognyan Oreshkov and Todd A. Brun. ``Weak measurements are universal''. Phys. Rev. Lett. 95, 110409 (2005). arXiv:quant-ph/0503017.
https://doi.org/10.1103/PhysRevLett.95.110409
arXiv:quant-ph/0503017

[35] Albert Schmid. ``Diffusion and localization in a dissipative quantum system''. Phys. Rev. Lett. 51, 1506–1509 (1983).
https://doi.org/10.1103/PhysRevLett.51.1506

[36] Matthew P. A. Fisher and Wilhelm Zwerger. ``Quantum brownian motion in a periodic potential''. Phys. Rev. B 32, 6190–6206 (1985).
https://doi.org/10.1103/PhysRevB.32.6190

[37] C. Aslangul, N. Pottier, and D. Saint-James. ``Quantum ohmic dissipation: Particle on a one-dimensional periodic lattice''. Physics Letters A 111, 175–178 (1985).
https://doi.org/10.1016/0375-9601(85)90570-5

[38] Tillmann Baumgratz, Marcus Cramer, and Martin B Plenio. ``Quantifying coherence''. Phys. Rev. Lett. 113, 140401 (2014). arXiv:1311.0275.
https://doi.org/10.1103/PhysRevLett.113.140401
arXiv:1311.0275

[39] Pavel A. Cherenkov. ``Visible luminescence of pure liquids under the influence of γ-radiation''. Dokl. Akad. Nauk SSSR 2, 451–454 (1934).
https://doi.org/10.3367/UFNr.0093.196710n.0385

[40] William G. Unruh. ``Notes on black-hole evaporation''. Phys. Rev. D 14, 870–892 (1976).
https://doi.org/10.1103/PhysRevD.14.870

[41] Yakir Aharonov and Leonard Susskind. ``Charge Superselection Rule''. Phys. Rev. 155, 1428–1431 (1967).
https://doi.org/10.1103/PhysRev.155.1428

[42] Carlo Rovelli. ``Relational quantum mechanics''. International journal of theoretical physics 35, 1637–1678 (1996).
https://doi.org/10.1007/BF02302261

[43] Stephen D. Bartlett, Terry Rudolph, and Robert W. Spekkens. ``Reference frames, superselection rules, and quantum information''. Rev. Mod. Phys. 79, 555–609 (2007). arXiv:quant-ph/0610030.
https://doi.org/10.1103/RevModPhys.79.555
arXiv:quant-ph/0610030

[44] B. N. Katz, M. P. Blencowe, and K. C. Schwab. ``Mesoscopic mechanical resonators as quantum noninertial reference frames''. Phys. Rev. A 92, 042104 (2015). arXiv:1409.2137.
https://doi.org/10.1103/PhysRevA.92.042104
arXiv:1409.2137

[45] Flaminia Giacomini, Esteban Castro-Ruiz, and Časlav Brukner. ``Quantum mechanics and the covariance of physical laws in quantum reference frames''. Nat. Commun. 10, 494 (2019). arXiv:1712.07207.
https://doi.org/10.1038/s41467-018-08155-0
arXiv:1712.07207

Cited by

[1] Matthew J. Lake and Marek Miller, "Quantum reference frames, revisited", arXiv:2312.03811, (2023).

The above citations are from SAO/NASA ADS (last updated successfully 2024-05-19 01:26:46). The list may be incomplete as not all publishers provide suitable and complete citation data.

On Crossref's cited-by service no data on citing works was found (last attempt 2024-05-19 01:26:45).

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.