Improved Quantum Query Complexity on Easier Inputs
1Middlebury College, Middlebury, VT, USA
2Williams College, Williamstown, MA, USA
3Brown University, Providence, RI, USA
| Published: | 2024-04-08, volume 8, page 1309 |
| Eprint: | arXiv:2303.00217v3 |
| Doi: | https://doi.org/10.22331/q-2024-04-08-1309 |
| Citation: | Quantum 8, 1309 (2024). |
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
Quantum span program algorithms for function evaluation sometimes have reduced query complexity when promised that the input has a certain structure. We design a modified span program algorithm to show these improvements persist even without a promise ahead of time, and we extend this approach to the more general problem of state conversion. As an application, we prove exponential and superpolynomial quantum advantages in average query complexity for several search problems, generalizing Montanaro's Search with Advice [Montanaro, TQC 2010].
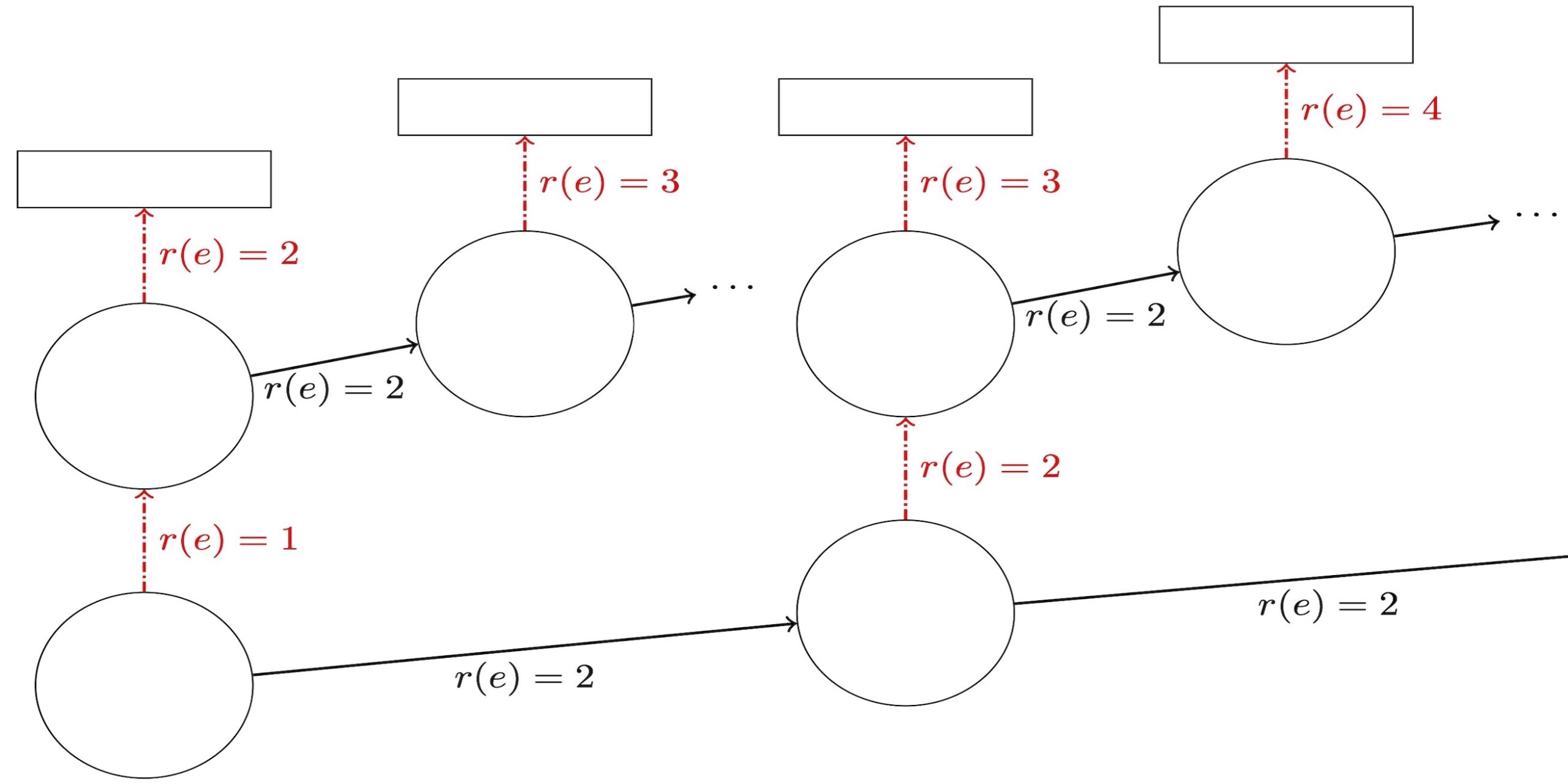
Featured image: Decision tree used to create one of our algorithms.
Popular summary
► BibTeX data
► References
[1] Andris Ambainis and Ronald de Wolf. Average-case quantum query complexity. Journal of Physics A: Mathematical and General, 34(35):6741, 2001. doi:10.1088/0305-4470/34/35/302.
https://doi.org/10.1088/0305-4470/34/35/302
[2] Dorit Aharonov. Quantum Computation. Annual Reviews of Computational Physics VI, pages 259–346, 1999. doi:10.1142/9789812815569_0007.
https://doi.org/10.1142/9789812815569_0007
[3] Michel Boyer, Gilles Brassard, Peter Høyer, and Alain Tapp. Tight Bounds on Quantum Searching. Fortschritte der Physik, 46(4-5):493–505, 1998. doi:10.1002/(SICI)1521-3978(199806)46:4/5<493::AID-PROP493>3.0.CO;2-P.
https://doi.org/10.1002/(SICI)1521-3978(199806)46:4/5<493::AID-PROP493>3.0.CO;2-P
[4] Aleksandrs Belovs. Span programs for functions with constant-sized 1-certificates: Extended abstract. In Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing, STOC '12, pages 77–84, 2012. doi:10.1145/2213977.2213985.
https://doi.org/10.1145/2213977.2213985
[5] Gilles Brassard, Peter Høyer, Michele Mosca, and Alain Tapp. Quantum amplitude amplification and estimation. In Quantum computation and information, volume 305 of Contemp. Math., pages 53–74. Amer. Math. Soc., Providence, RI, 2002. doi:10.1090/conm/305/05215.
https://doi.org/10.1090/conm/305/05215
[6] Gilles Brassard, Peter Høyer, and Alain Tapp. Quantum counting. In Automata, Languages and Programming, pages 820–831, 1998. doi:10.1007/BFb0055105.
https://doi.org/10.1007/BFb0055105
[7] Aleksandrs Belovs and Ben W. Reichardt. Span programs and quantum algorithms for st-connectivity and claw detection. Lecture Notes in Computer Science, 7501 LNCS:193–204, 2012. doi:10.1007/978-3-642-33090-2_18.
https://doi.org/10.1007/978-3-642-33090-2_18
[8] Aleksandrs Belovs and Ansis Rosmanis. Tight Quantum Lower Bound for Approximate Counting with Quantum States. 2020. arXiv:2002.06879.
arXiv:2002.06879
[9] Salman Beigi and Leila Taghavi. Quantum speedup based on classical decision trees. Quantum, 4:241, 2020. doi:10.22331/q-2020-03-02-241.
https://doi.org/10.22331/q-2020-03-02-241
[10] Aleksandrs Belovs and Duyal Yolcu. One-way ticket to las vegas and the quantum adversary. 2023. arXiv:2301.02003.
arXiv:2301.02003
[11] Richard. Cleve, Artur. Ekert, Chiara Macchiavello, and Michele Mosca. Quantum algorithms revisited. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 454(1969):339–354, 1998. doi:10.1098/rspa.1998.0164.
https://doi.org/10.1098/rspa.1998.0164
[12] Arjan Cornelissen, Stacey Jeffery, Maris Ozols, and Alvaro Piedrafita. Span programs and quantum time complexity. In 45th International Symposium on Mathematical Foundations of Computer Science (MFCS 2020). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2020. doi:10.4230/LIPIcs.MFCS.2020.26.
https://doi.org/10.4230/LIPIcs.MFCS.2020.26
[13] Chris Cade, Ashley Montanaro, and Aleksandrs Belovs. Time and space efficient quantum algorithms for detecting cycles and testing bipartiteness. Quantum Information & Computation, 18(1-2):18–50, 2018.
[14] Kai DeLorenzo, Shelby Kimmel, and R. Teal Witter. Applications of the Quantum Algorithm for st-Connectivity. In 14th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2019), pages 6:1–6:14, 2019. doi:10.4230/LIPIcs.TQC.2019.6.
https://doi.org/10.4230/LIPIcs.TQC.2019.6
[15] Dmitry Grinko, Julien Gacon, Christa Zoufal, and Stefan Woerner. Iterative quantum amplitude estimation. npj Quantum Information, 7(1):52, Mar 2021. doi:10.1038/s41534-021-00379-1.
https://doi.org/10.1038/s41534-021-00379-1
[16] Lov K. Grover. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Physical Review Letters, 79(2):325–328, 1997. doi:10.1103/PhysRevLett.79.325.
https://doi.org/10.1103/PhysRevLett.79.325
[17] Wassily Hoeffding. Probability inequalities for sums of bounded random variables. Journal of the American Statistical Association, 58(301):13–30, 1963. doi:10.1080/01621459.1963.10500830.
https://doi.org/10.1080/01621459.1963.10500830
[18] Tsuyoshi Ito and Stacey Jeffery. Approximate Span Programs. Algorithmica, 81(6):2158–2195, 2019. doi:10.1007/s00453-018-0527-1.
https://doi.org/10.1007/s00453-018-0527-1
[19] Michael Jarret, Stacey Jeffery, Shelby Kimmel, and Alvaro Piedrafita. Quantum Algorithms for Connectivity and Related Problems. In 26th Annual European Symposium on Algorithms (ESA 2018), pages 49:1–49:13, 2018. doi:10.4230/LIPIcs.ESA.2018.49.
https://doi.org/10.4230/LIPIcs.ESA.2018.49
[20] Alexei Y. Kitaev. Quantum measurements and the Abelian Stabilizer Problem. 1995. arXiv:quant-ph/9511026.
arXiv:quant-ph/9511026
[21] Troy Lee, Rajat Mittal, Ben W. Reichardt, Robert Špalek, and Mario Szegedy. Quantum Query Complexity of State Conversion. In 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, pages 344–353, 2011. doi:10.1109/FOCS.2011.75.
https://doi.org/10.1109/FOCS.2011.75
[22] Frédéric Magniez, Ashwin Nayak, Jérémie Roland, and Miklos Santha. Search via Quantum Walk. SIAM Journal on Computing, 40(1):142–164, 2011. doi:10.1137/090745854.
https://doi.org/10.1137/090745854
[23] Ashley Montanaro. Quantum search with advice. In Conference on Quantum Computation, Communication, and Cryptography, pages 77–93. Springer, 2010. doi:10.1007/978-3-642-18073-6_7.
https://doi.org/10.1007/978-3-642-18073-6_7
[24] Ben W. Reichardt. Span programs and quantum query complexity: The general adversary bound is nearly tight for every boolean function. 50th Annual IEEE Symposium on Foundations of Computer Science, pages 544–551, 2009. doi:10.1109/FOCS.2009.55.
https://doi.org/10.1109/FOCS.2009.55
[25] Ben W. Reichardt. Reflections for quantum query algorithms. In Proceedings of the 2011 Annual ACM-SIAM Symposium on Discrete Algorithms, Proceedings, pages 560–569. 2011. doi:10.1137/1.9781611973082.44.
https://doi.org/10.1137/1.9781611973082.44
[26] Leila Taghavi. Simplified quantum algorithm for the oracle identification problem. Quantum Machine Intelligence, 4(2):19, 2022. doi:10.1007/s42484-022-00080-2.
https://doi.org/10.1007/s42484-022-00080-2
Cited by
[1] Stacey Jeffery, Shelby Kimmel, and Alvaro Piedrafita, "Quantum Algorithm for Path-Edge Sampling", arXiv:2303.03319, (2023).
[2] Michael Czekanski, Shelby Kimmel, and R. Teal Witter, "Robust and Space-Efficient Dual Adversary Quantum Query Algorithms", arXiv:2306.15040, (2023).
The above citations are from SAO/NASA ADS (last updated successfully 2024-05-13 07:22:37). The list may be incomplete as not all publishers provide suitable and complete citation data.
On Crossref's cited-by service no data on citing works was found (last attempt 2024-05-13 07:22:36).
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.