Rapid quantum approaches for combinatorial optimisation inspired by optimal state-transfer
1London Centre for Nanotechnology, UCL, London WC1H 0AH, UK
2Department of Physics and Astronomy, UCL, London WC1E 6BT, UK
3Department of Electronic & Electrical Engineering, UCL, London WC1E 7JE, UK
| Published: | 2024-02-13, volume 8, page 1253 |
| Eprint: | arXiv:2301.06846v2 |
| Doi: | https://doi.org/10.22331/q-2024-02-13-1253 |
| Citation: | Quantum 8, 1253 (2024). |
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
We propose a new design heuristic to tackle combinatorial optimisation problems, inspired by Hamiltonians for optimal state-transfer. The result is a rapid approximate optimisation algorithm. We provide numerical evidence of the success of this new design heuristic. We find this approach results in a better approximation ratio than the Quantum Approximate Optimisation Algorithm at lowest depth for the majority of problem instances considered, while utilising comparable resources. This opens the door to investigating new approaches for tackling combinatorial optimisation problems, distinct from adiabatic-influenced approaches.
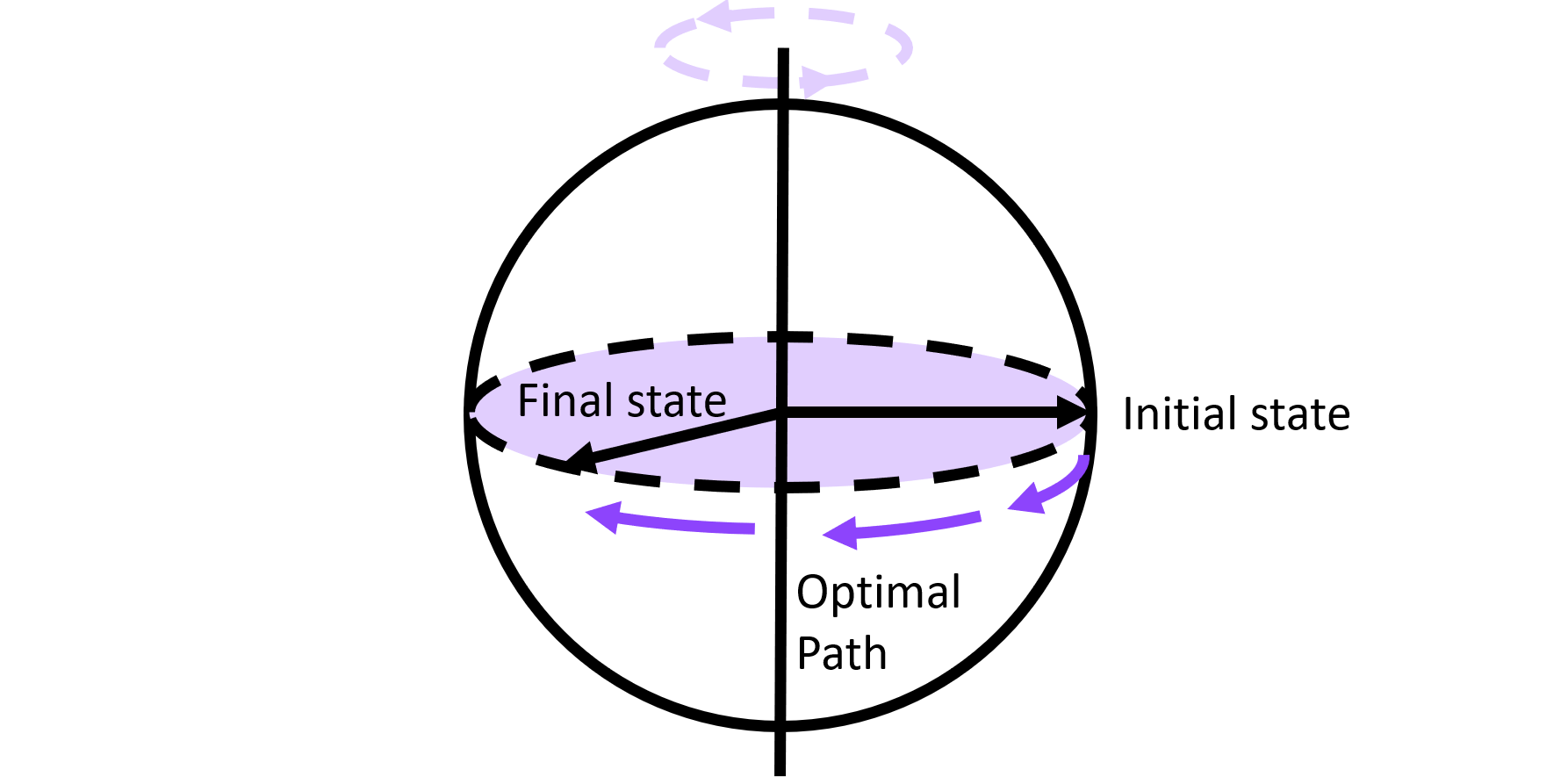
Popular summary
Quantum algorithms for tackling combinatorial optimisation problems are typically influenced by the adiabatic principle. In short, by going sufficiently slowly it is possible to get from the starting state to the final state. This can result in long run times for the algorithm.
To assess the performance of our new approach we examined its performance on MAX-CUT. We also compared our new approach to the popular Quantum Approximate Optimisation Algorithm (QAOA) in a regime where it utilizes similar resources. Not only did our new approach find better quality solutions, it found them in a shorter time with less classical computational overhead.
Our work opens the door to exploring quantum algorithm design, away from the adiabatic principle, for combinatorial optimisation problems. In the future this new approach might be combined with adiabatic approaches in the development of more sophisticated quantum algorithms.
► BibTeX data
► References
[1] Christos H. Papadimitriou and Kenneth Steiglitz. ``Combinatorial optimization: Algorithms and complexity''. Dover Publications. (1981).
[2] M. H. S. Amin. ``Consistency of the adiabatic theorem''. Phys. Rev. Lett. 102, 220401 (2009).
https://doi.org/10.1103/PhysRevLett.102.220401
[3] Ben W. Reichardt. ``The quantum adiabatic optimization algorithm and local minima''. In Proceedings of the Thirty-Sixth Annual ACM Symposium on Theory of Computing. Page 502–510. STOC '04New York, NY, USA (2004). Association for Computing Machinery.
https://doi.org/10.1145/1007352.1007428
[4] B. Apolloni, C. Carvalho, and D. de Falco. ``Quantum stochastic optimization''. Stochastic Processes and their Applications 33, 233–244 (1989).
https://doi.org/10.1016/0304-4149(89)90040-9
[5] Edward Farhi, Jeffrey Goldstone, Sam Gutmann, and Michael Sipser. ``Quantum computation by adiabatic evolution'' (2000).
arXiv:quant-ph/0001106
[6] Tadashi Kadowaki and Hidetoshi Nishimori. ``Quantum annealing in the transverse ising model''. Phys. Rev. E 58, 5355–5363 (1998).
https://doi.org/10.1103/PhysRevE.58.5355
[7] A.B. Finnila, M.A. Gomez, C. Sebenik, C. Stenson, and J.D. Doll. ``Quantum annealing: A new method for minimizing multidimensional functions''. Chemical Physics Letters 219, 343–348 (1994).
https://doi.org/10.1016/0009-2614(94)00117-0
[8] Tameem Albash and Daniel A. Lidar. ``Adiabatic quantum computation''. Reviews of Modern Physics 90 (2018).
https://doi.org/10.1103/revmodphys.90.015002
[9] N. G. Dickson, M. W. Johnson, M. H. Amin, R. Harris, F. Altomare, A. J. Berkley, P. Bunyk, J. Cai, E. M. Chapple, P. Chavez, F. Cioata, T. Cirip, P. deBuen, M. Drew-Brook, C. Enderud, S. Gildert, F. Hamze, J. P. Hilton, E. Hoskinson, K. Karimi, E. Ladizinsky, N. Ladizinsky, T. Lanting, T. Mahon, R. Neufeld, T. Oh, I. Perminov, C. Petroff, A. Przybysz, C. Rich, P. Spear, A. Tcaciuc, M. C. Thom, E. Tolkacheva, S. Uchaikin, J. Wang, A. B. Wilson, Z. Merali, and G. Rose. ``Thermally assisted quantum annealing of a 16-qubit problem''. Nature Communications 4, 1903 (2013).
https://doi.org/10.1038/ncomms2920
[10] E. J. Crosson and D. A. Lidar. ``Prospects for quantum enhancement with diabatic quantum annealing''. Nature Reviews Physics 3, 466–489 (2021).
https://doi.org/10.1038/s42254-021-00313-6
[11] Louis Fry-Bouriaux, Daniel T. O'Connor, Natasha Feinstein, and Paul A. Warburton. ``Locally suppressed transverse-field protocol for diabatic quantum annealing''. Phys. Rev. A 104, 052616 (2021).
https://doi.org/10.1103/PhysRevA.104.052616
[12] Rolando D. Somma, Daniel Nagaj, and Mária Kieferová. ``Quantum speedup by quantum annealing''. Phys. Rev. Lett. 109, 050501 (2012).
https://doi.org/10.1103/PhysRevLett.109.050501
[13] Edward Farhi, Jeffrey Goldston, David Gosset, Sam Gutmann, Harvey B. Meyer, and Peter Shor. ``Quantum adiabatic algorithms, small gaps, and different paths''. Quantum Info. Comput. 11, 181–214 (2011).
https://doi.org/10.26421/qic11.3-4-1
[14] Lishan Zeng, Jun Zhang, and Mohan Sarovar. ``Schedule path optimization for adiabatic quantum computing and optimization''. Journal of Physics A: Mathematical and Theoretical 49, 165305 (2016).
https://doi.org/10.1088/1751-8113/49/16/165305
[15] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. ``Quantum adiabatic evolution algorithms with different paths'' (2002). arXiv:quant-ph/0208135.
arXiv:quant-ph/0208135
[16] Natasha Feinstein, Louis Fry-Bouriaux, Sougato Bose, and P. A. Warburton. ``Effects of xx-catalysts on quantum annealing spectra with perturbative crossings'' (2022). arXiv:2203.06779.
arXiv:2203.06779
[17] Elizabeth Crosson, Edward Farhi, Cedric Yen-Yu Lin, Han-Hsuan Lin, and Peter Shor. ``Different strategies for optimization using the quantum adiabatic algorithm'' (2014). arXiv:1401.7320.
arXiv:1401.7320
[18] Vicky Choi. ``Essentiality of the non-stoquastic hamiltonians and driver graph design in quantum optimization annealing'' (2021). arXiv:2105.02110.
arXiv:2105.02110
[19] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. ``A quantum approximate optimization algorithm'' (2014). arXiv:1411.4028.
arXiv:1411.4028
[20] Adam Callison, Nicholas Chancellor, Florian Mintert, and Viv Kendon. ``Finding spin glass ground states using quantum walks''. New Journal of Physics 21, 123022 (2019).
https://doi.org/10.1088/1367-2630/ab5ca2
[21] Viv Kendon. ``How to compute using quantum walks''. Electronic Proceedings in Theoretical Computer Science 315, 1–17 (2020).
https://doi.org/10.4204/eptcs.315.1
[22] Adam Callison, Max Festenstein, Jie Chen, Laurentiu Nita, Viv Kendon, and Nicholas Chancellor. ``Energetic perspective on rapid quenches in quantum annealing''. PRX Quantum 2, 010338 (2021).
https://doi.org/10.1103/PRXQuantum.2.010338
[23] James G. Morley, Nicholas Chancellor, Sougato Bose, and Viv Kendon. ``Quantum search with hybrid adiabatic–quantum-walk algorithms and realistic noise''. Physical Review A 99 (2019).
https://doi.org/10.1103/physreva.99.022339
[24] Dorje C Brody and Daniel W Hook. ``On optimum hamiltonians for state transformations''. Journal of Physics A: Mathematical and General 39, L167–L170 (2006).
https://doi.org/10.1088/0305-4470/39/11/l02
[25] J.R. Johansson, P.D. Nation, and Franco Nori. ``Qutip: An open-source python framework for the dynamics of open quantum systems''. Computer Physics Communications 183, 1760–1772 (2012).
https://doi.org/10.1016/j.cpc.2012.02.021
[26] J.R. Johansson, P.D. Nation, and Franco Nori. ``Qutip 2: A python framework for the dynamics of open quantum systems''. Computer Physics Communications 184, 1234–1240 (2013).
https://doi.org/10.1016/j.cpc.2012.11.019
[27] MD Sajid Anis, Abby-Mitchell, Héctor Abraham, and AduOffei et al. ``Qiskit: An open-source framework for quantum computing'' (2021).
[28] John Preskill. ``Quantum computing in the NISQ era and beyond''. Quantum 2, 79 (2018).
https://doi.org/10.22331/q-2018-08-06-79
[29] Philipp Hauke, Helmut G Katzgraber, Wolfgang Lechner, Hidetoshi Nishimori, and William D Oliver. ``Perspectives of quantum annealing: methods and implementations''. Reports on Progress in Physics 83, 054401 (2020).
https://doi.org/10.1088/1361-6633/ab85b8
[30] Leo Zhou, Sheng-Tao Wang, Soonwon Choi, Hannes Pichler, and Mikhail D. Lukin. ``Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices''. Phys. Rev. X 10, 021067 (2020).
https://doi.org/10.1103/PhysRevX.10.021067
[31] Stuart Hadfield, Zhihui Wang, Bryan O'Gorman, Eleanor Rieffel, Davide Venturelli, and Rupak Biswas. ``From the quantum approximate optimization algorithm to a quantum alternating operator ansatz''. Algorithms 12, 34 (2019).
https://doi.org/10.3390/a12020034
[32] Matthew P. Harrigan, Kevin J. Sung, Matthew Neeley, and Kevin J. Satzinger et al. ``Quantum approximate optimization of non-planar graph problems on a planar superconducting processor''. Nature Physics 17, 332–336 (2021).
https://doi.org/10.1038/s41567-020-01105-y
[33] T. M. Graham, Y. Song, J. Scott, C. Poole, L. Phuttitarn, K. Jooya, P. Eichler, X. Jiang, A. Marra, B. Grinkemeyer, M. Kwon, M. Ebert, J. Cherek, M. T. Lichtman, M. Gillette, J. Gilbert, D. Bowman, T. Ballance, C. Campbell, E. D. Dahl, O. Crawford, N. S. Blunt, B. Rogers, T. Noel, and M. Saffman. ``Multi-qubit entanglement and algorithms on a neutral-atom quantum computer''. Nature 604, 457–462 (2022).
https://doi.org/10.1038/s41586-022-04603-6
[34] J. S. Otterbach, R. Manenti, N. Alidoust, A. Bestwick, M. Block, B. Bloom, S. Caldwell, N. Didier, E. Schuyler Fried, S. Hong, P. Karalekas, C. B. Osborn, A. Papageorge, E. C. Peterson, G. Prawiroatmodjo, N. Rubin, Colm A. Ryan, D. Scarabelli, M. Scheer, E. A. Sete, P. Sivarajah, Robert S. Smith, A. Staley, N. Tezak, W. J. Zeng, A. Hudson, Blake R. Johnson, M. Reagor, M. P. da Silva, and C. Rigetti. ``Unsupervised machine learning on a hybrid quantum computer'' (2017). arXiv:1712.05771.
arXiv:1712.05771
[35] Lucas T. Brady, Christopher L. Baldwin, Aniruddha Bapat, Yaroslav Kharkov, and Alexey V. Gorshkov. ``Optimal protocols in quantum annealing and quantum approximate optimization algorithm problems''. Phys. Rev. Lett. 126, 070505 (2021).
https://doi.org/10.1103/PhysRevLett.126.070505
[36] Lucas T. Brady, Lucas Kocia, Przemyslaw Bienias, Aniruddha Bapat, Yaroslav Kharkov, and Alexey V. Gorshkov. ``Behavior of analog quantum algorithms'' (2021). arXiv:2107.01218.
arXiv:2107.01218
[37] Xinyu Fei, Lucas T. Brady, Jeffrey Larson, Sven Leyffer, and Siqian Shen. ``Binary control pulse optimization for quantum systems''. Quantum 7, 892 (2023).
https://doi.org/10.22331/q-2023-01-04-892
[38] Lorenzo Campos Venuti, Domenico D'Alessandro, and Daniel A. Lidar. ``Optimal control for quantum optimization of closed and open systems''. Physical Review Applied 16 (2021).
https://doi.org/10.1103/physrevapplied.16.054023
[39] M.A. Nielsen. ``A geometric approach to quantum circuit lower bounds''. Quantum Information and Computation 6, 213–262 (2006).
https://doi.org/10.26421/qic6.3-2
[40] Michael A. Nielsen, Mark R. Dowling, Mile Gu, and Andrew C. Doherty. ``Quantum computation as geometry''. Science 311, 1133–1135 (2006).
https://doi.org/10.1126/science.1121541
[41] M.R. Dowling and M.A. Nielsen. ``The geometry of quantum computation''. Quantum Information and Computation 8, 861–899 (2008).
https://doi.org/10.26421/qic8.10-1
[42] Alberto Carlini, Akio Hosoya, Tatsuhiko Koike, and Yosuke Okudaira. ``Time-optimal quantum evolution''. Phys. Rev. Lett. 96, 060503 (2006).
https://doi.org/10.1103/PhysRevLett.96.060503
[43] Alberto Carlini, Akio Hosoya, Tatsuhiko Koike, and Yosuke Okudaira. ``Time-optimal unitary operations''. Physical Review A 75 (2007).
https://doi.org/10.1103/physreva.75.042308
[44] A. T. Rezakhani, W.-J. Kuo, A. Hamma, D. A. Lidar, and P. Zanardi. ``Quantum adiabatic brachistochrone''. Physical Review Letters 103 (2009).
https://doi.org/10.1103/physrevlett.103.080502
[45] Xiaoting Wang, Michele Allegra, Kurt Jacobs, Seth Lloyd, Cosmo Lupo, and Masoud Mohseni. ``Quantum brachistochrone curves as geodesics: Obtaining accurate minimum-time protocols for the control of quantum systems''. Phys. Rev. Lett. 114, 170501 (2015).
https://doi.org/10.1103/PhysRevLett.114.170501
[46] Hiroaki Wakamura and Tatsuhiko Koike. ``A general formulation of time-optimal quantum control and optimality of singular protocols''. New Journal of Physics 22, 073010 (2020).
https://doi.org/10.1088/1367-2630/ab8ab3
[47] Ding Wang, Haowei Shi, and Yueheng Lan. ``Quantum brachistochrone for multiple qubits''. New Journal of Physics 23, 083043 (2021).
https://doi.org/10.1088/1367-2630/ac1df5
[48] Alan C. Santos, C. J. Villas-Boas, and R. Bachelard. ``Quantum adiabatic brachistochrone for open systems''. Phys. Rev. A 103, 012206 (2021).
https://doi.org/10.1103/PhysRevA.103.012206
[49] Jing Yang and Adolfo del Campo. ``Minimum-time quantum control and the quantum brachistochrone equation'' (2022). arXiv:2204.12792.
arXiv:2204.12792
[50] J. Anandan and Y. Aharonov. ``Geometry of quantum evolution''. Phys. Rev. Lett. 65, 1697–1700 (1990).
https://doi.org/10.1103/PhysRevLett.65.1697
[51] Alberto Peruzzo, Jarrod McClean, Peter Shadbolt, Man-Hong Yung, Xiao-Qi Zhou, Peter J. Love, Alán Aspuru-Guzik, and Jeremy L. O'Brien. ``A variational eigenvalue solver on a photonic quantum processor''. Nature Communications 5, 4213 (2014).
https://doi.org/10.1038/ncomms5213
[52] Dmitry A. Fedorov, Bo Peng, Niranjan Govind, and Yuri Alexeev. ``VQE method: a short survey and recent developments''. Materials Theory 6 (2022).
https://doi.org/10.1186/s41313-021-00032-6
[53] Li Li, Minjie Fan, Marc Coram, Patrick Riley, and Stefan Leichenauer. ``Quantum optimization with a novel gibbs objective function and ansatz architecture search''. Phys. Rev. Research 2, 023074 (2020).
https://doi.org/10.1103/PhysRevResearch.2.023074
[54] Panagiotis Kl. Barkoutsos, Giacomo Nannicini, Anton Robert, Ivano Tavernelli, and Stefan Woerner. ``Improving variational quantum optimization using CVaR''. Quantum 4, 256 (2020).
https://doi.org/10.22331/q-2020-04-20-256
[55] Dorje C. Brody and David M. Meier. ``Solution to the quantum zermelo navigation problem''. Phys. Rev. Lett. 114, 100502 (2015).
https://doi.org/10.1103/PhysRevLett.114.100502
[56] Dorje C Brody, Gary W Gibbons, and David M Meier. ``Time-optimal navigation through quantum wind''. New Journal of Physics 17, 033048 (2015).
https://doi.org/10.1088/1367-2630/17/3/033048
[57] Benjamin Russell and Susan Stepney. ``Zermelo navigation and a speed limit to quantum information processing''. Phys. Rev. A 90, 012303 (2014).
https://doi.org/10.1103/PhysRevA.90.012303
[58] Benjamin Russell and Susan Stepney. ``Zermelo navigation in the quantum brachistochrone''. Journal of Physics A: Mathematical and Theoretical 48, 115303 (2015).
https://doi.org/10.1088/1751-8113/48/11/115303
[59] Sergey Bravyi and Barbara Terhal. ``Complexity of stoquastic frustration-free hamiltonians''. SIAM Journal on Computing 39, 1462–1485 (2010).
https://doi.org/10.1137/08072689X
[60] Glen Bigan Mbeng, Rosario Fazio, and Giuseppe Santoro. ``Quantum annealing: a journey through digitalization, control, and hybrid quantum variational schemes'' (2019). arXiv:1906.08948.
arXiv:1906.08948
[61] Arthur Braida, Simon Martiel, and Ioan Todinca. ``On constant-time quantum annealing and guaranteed approximations for graph optimization problems''. Quantum Science and Technology 7, 045030 (2022).
https://doi.org/10.1088/2058-9565/ac8e91
[62] Alexey Galda, Xiaoyuan Liu, Danylo Lykov, Yuri Alexeev, and Ilya Safro. ``Transferability of optimal qaoa parameters between random graphs''. In 2021 IEEE International Conference on Quantum Computing and Engineering (QCE). Pages 171–180. (2021).
https://doi.org/10.1109/QCE52317.2021.00034
[63] M. Lapert, Y. Zhang, M. Braun, S. J. Glaser, and D. Sugny. ``Singular extremals for the time-optimal control of dissipative spin $\frac{1}{2}$ particles''. Phys. Rev. Lett. 104, 083001 (2010).
https://doi.org/10.1103/PhysRevLett.104.083001
[64] Victor Mukherjee, Alberto Carlini, Andrea Mari, Tommaso Caneva, Simone Montangero, Tommaso Calarco, Rosario Fazio, and Vittorio Giovannetti. ``Speeding up and slowing down the relaxation of a qubit by optimal control''. Phys. Rev. A 88, 062326 (2013).
https://doi.org/10.1103/PhysRevA.88.062326
[65] D. Guéry-Odelin, A. Ruschhaupt, A. Kiely, E. Torrontegui, S. Martínez-Garaot, and J. G. Muga. ``Shortcuts to adiabaticity: Concepts, methods, and applications''. Rev. Mod. Phys. 91, 045001 (2019).
https://doi.org/10.1103/RevModPhys.91.045001
[66] Elliott H. Lieb and Derek W. Robinson. ``The finite group velocity of quantum spin systems''. Communications in Mathematical Physics 28, 251–257 (1972).
https://doi.org/10.1007/BF01645779
[67] Zhiyuan Wang and Kaden R.A. Hazzard. ``Tightening the lieb-robinson bound in locally interacting systems''. PRX Quantum 1, 010303 (2020).
https://doi.org/10.1103/PRXQuantum.1.010303
[68] Andrew M. Childs and Nathan Wiebe. ``Product formulas for exponentials of commutators''. Journal of Mathematical Physics 54, 062202 (2013).
https://doi.org/10.1063/1.4811386
[69] Wolfgang Lechner, Philipp Hauke, and Peter Zoller. ``A quantum annealing architecture with all-to-all connectivity from local interactions''. Science Advances 1 (2015).
https://doi.org/10.1126/sciadv.1500838
[70] Nicholas Chancellor. ``Domain wall encoding of discrete variables for quantum annealing and QAOA''. Quantum Science and Technology 4, 045004 (2019).
https://doi.org/10.1088/2058-9565/ab33c2
[71] Helmut G. Katzgraber, Firas Hamze, Zheng Zhu, Andrew J. Ochoa, and H. Munoz-Bauza. ``Seeking quantum speedup through spin glasses: The good, the bad, and the ugly''. Physical Review X 5 (2015).
https://doi.org/10.1103/physrevx.5.031026
[72] M.R. Garey, D.S. Johnson, and L. Stockmeyer. ``Some simplified np-complete graph problems''. Theoretical Computer Science 1, 237–267 (1976).
https://doi.org/10.1016/0304-3975(76)90059-1
[73] Christos H. Papadimitriou and Mihalis Yannakakis. ``Optimization, approximation, and complexity classes''. Journal of Computer and System Sciences 43, 425–440 (1991).
https://doi.org/10.1016/0022-0000(91)90023-X
[74] Zhihui Wang, Stuart Hadfield, Zhang Jiang, and Eleanor G. Rieffel. ``Quantum approximate optimization algorithm for MaxCut: A fermionic view''. Physical Review A 97 (2018).
https://doi.org/10.1103/physreva.97.022304
[75] Glen Bigan Mbeng, Angelo Russomanno, and Giuseppe E. Santoro. ``The quantum ising chain for beginners'' (2020). arXiv:2009.09208.
arXiv:2009.09208
[76] David Gamarnik and Quan Li. ``On the max-cut of sparse random graphs''. Random Structures & Algorithms 52, 219–262 (2018).
https://doi.org/10.1002/rsa.20738
[77] Don Coppersmith, David Gamarnik, MohammadTaghi Hajiaghayi, and Gregory B. Sorkin. ``Random max sat, random max cut, and their phase transitions''. Random Structures & Algorithms 24, 502–545 (2004).
https://doi.org/10.1002/rsa.20015
[78] Anthony Polloreno and Graeme Smith. ``The qaoa with slow measurements'' (2022). arXiv:2205.06845.
arXiv:2205.06845
[79] David Sherrington and Scott Kirkpatrick. ``Solvable model of a spin-glass''. Phys. Rev. Lett. 35, 1792–1796 (1975).
https://doi.org/10.1103/PhysRevLett.35.1792
[80] Tadashi Kadowaki and Hidetoshi Nishimori. ``Greedy parameter optimization for diabatic quantum annealing''. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 381 (2022).
https://doi.org/10.1098/rsta.2021.0416
[81] J. D. Hunter. ``Matplotlib: A 2d graphics environment''. Computing in Science & Engineering 9, 90–95 (2007).
https://doi.org/10.1109/MCSE.2007.55
[82] Frederik Michel Dekking, Cornelis Kraaikamp, Hendrik Paul Lopuhaä, and Ludolf Erwin Meester. ``A modern introduction to probability and statistics''. Springer London. (2005).
https://doi.org/10.1007/1-84628-168-7
[83] K. F. Riley, Marcella Paola Hobson, and Stephen Bence. ``Mathematical methods for physics and engineering - 3rd edition''. Cambridge University Press. (2006).
https://doi.org/10.1017/CBO9780511810763
Cited by
[1] Arthur Braida, Simon Martiel, and Ioan Todinca, "Tight Lieb–Robinson Bound for approximation ratio in quantum annealing", npj Quantum Information 10 1, 40 (2024).
[2] Boniface Yogendran, Daniel Charlton, Miriam Beddig, Ioannis Kolotouros, and Petros Wallden, "Big data applications on small quantum computers", arXiv:2402.01529, (2024).
[3] Lasse Gerblich, Tamanna Dasanjh, Horatio Q. X. Wong, David Ross, Leonardo Novo, Nicholas Chancellor, and Viv Kendon, "Advantages of multistage quantum walks over QAOA", arXiv:2407.06663, (2024).
The above citations are from Crossref's cited-by service (last updated successfully 2024-07-26 21:34:30) and SAO/NASA ADS (last updated successfully 2024-07-26 21:34:31). The list may be incomplete as not all publishers provide suitable and complete citation data.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.