Adaptive Quantum State Tomography with Active Learning
1Department of Physics and Arnold Sommerfeld Center for Theoretical Physics (ASC), Ludwig-Maximilians-Universität München, Theresienstr. 37, München D-80333, Germany
2Munich Center for Quantum Science and Technology (MCQST), Schellingstr. 4, D-80799 München, Germany
3ITAMP, Harvard-Smithsonian Center for Astrophysics, Cambridge, MA 02138, USA
4Department of Physics, Harvard University, Cambridge, MA 02138, USA
| Published: | 2023-10-09, volume 7, page 1129 |
| Eprint: | arXiv:2203.15719v6 |
| Doi: | https://doi.org/10.22331/q-2023-10-09-1129 |
| Citation: | Quantum 7, 1129 (2023). |
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
Recently, tremendous progress has been made in the field of quantum science and technologies: different platforms for quantum simulation as well as quantum computing, ranging from superconducting qubits to neutral atoms, are starting to reach unprecedentedly large systems. In order to benchmark these systems and gain physical insights, the need for efficient tools to characterize quantum states arises. The exponential growth of the Hilbert space with system size renders a full reconstruction of the quantum state prohibitively demanding in terms of the number of necessary measurements. Here we propose and implement an efficient scheme for quantum state tomography using active learning. Based on a few initial measurements, the active learning protocol proposes the next measurement basis, designed to yield the maximum information gain. We apply the active learning quantum state tomography scheme to reconstruct different multi-qubit states with varying degree of entanglement as well as to ground states of the XXZ model in 1D and a kinetically constrained spin chain. In all cases, we obtain a significantly improved reconstruction as compared to a reconstruction based on the exact same number of measurements and measurement configurations, but with randomly chosen basis configurations. Our scheme is highly relevant to gain physical insights in quantum many-body systems as well as for benchmarking and characterizing quantum devices, e.g. for quantum simulation, and paves the way for scalable adaptive protocols to probe, prepare, and manipulate quantum systems.
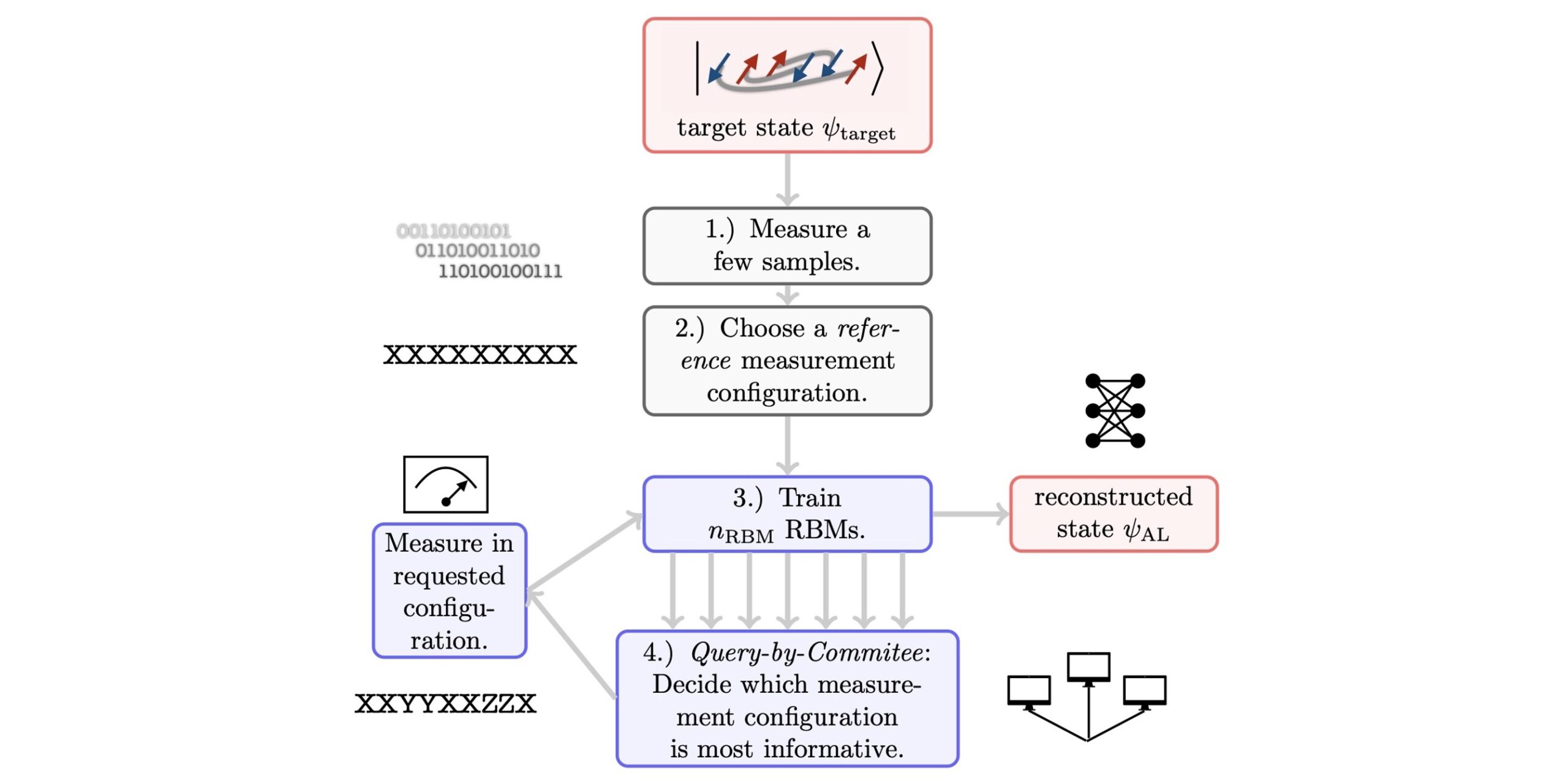
Featured image: The active learning protocol.
Popular summary
► BibTeX data
► References
[1] P. Nimbe, B. A. Weyori, and A. F. Adekoya. ``Models in quantum computing: a systematic review''. Quantum Information Processing 20 (2021).
https://doi.org/10.1007/s11128-021-03021-3
[2] I. Bloch, J. Dalibard, and S. Nascimbène. ``Quantum simulations with ultracold quantum gases''. Nature Physics 8 (2012).
https://doi.org/10.1038/nphys2259
[3] J. Preskill. ``Quantum computing in the nisq era and beyond''. Quantum 2, 79 (2018).
https://doi.org/10.22331/q-2018-08-06-79
[4] E. Altman, K. R. Brown, G. Carleo, L. D. Carr, E. Demler, C. Chin, B. DeMarco, S. E. Economou, M. A. Eriksson, K. C. Fu, M. Greiner, K. R.A. Hazzard, R. G. Hulet, A. J. Kollár, B. L. Lev, and authors. ``Quantum simulators: Architectures and opportunities''. PRX Quantum 2, 017003 (2021).
https://doi.org/10.1103/PRXQuantum.2.017003
[5] H. Häffner, W. Hänsel, C. F. Roos, J. Benhelm, D. Chek-al kar, M. Chwalla, T. Körber, U. D. Rapol, M. Riebe, P. O. Schmidt, C. Becher, O. Gühne, W. Dür, and R. Blatt. ``Scalable multiparticle entanglement of trapped ions''. Nature 438, 643–646 (2005).
https://doi.org/10.1038/nature04279
[6] Z. Hradil. ``Quantum-state estimation''. Phys. Rev. A 55, R1561–R1564 (1997).
https://doi.org/10.1103/PhysRevA.55.R1561
[7] Abhijith J., Adetokunbo Adedoyin, John Ambrosiano, Petr Anisimov, William Casper, Gopinath Chennupati, Carleton Coffrin, Hristo Djidjev, David Gunter, Satish Karra, Nathan Lemons, Shizeng Lin, Alexander Malyzhenkov, David Mascarenas, Susan Mniszewski, Balu Nadiga, Daniel O’malley, Diane Oyen, Scott Pakin, Lakshman Prasad, Randy Roberts, Phillip Romero, Nandakishore Santhi, Nikolai Sinitsyn, Pieter J. Swart, James G. Wendelberger, Boram Yoon, Richard Zamora, Wei Zhu, Stephan Eidenbenz, Andreas Bärtschi, Patrick J. Coles, Marc Vuffray, and Andrey Y. Lokhov. ``Quantum algorithm implementations for beginners''. ACM Transactions on Quantum Computing 3 (2022).
https://doi.org/10.1145/3517340
[8] T. Baumgratz, D. Gross, M. Cramer, and M. B. Plenio. ``Scalable reconstruction of density matrices''. Phys. Rev. Lett. 111, 020401 (2013).
https://doi.org/10.1103/PhysRevLett.111.020401
[9] B. P. Lanyon, C. Maier, M. Holzäpfel, T. Baumgratz, C. Hempel, P. Jurcevic, I. Dhand, A. S. Buyskikh, A. J. Daley, M. Cramer, M. B. Plenio, R. Blatt, and C. F. Roos. ``Efficient tomography of a quantum many-body system''. Nature Physics 13, 1745–2481 (2017).
https://doi.org/10.1038/nphys4244
[10] Giuseppe Carleo and Matthias Troyer. ``Solving the quantum many-body problem with artificial neural networks''. Science 355, 602–606 (2017).
https://doi.org/10.1126/science.aag2302
[11] G. Torlai, G. Mazzola, Ju. Carrasquilla, M. Troyer, R. Melko, and G. Carleo. ``Neural-network quantum state tomography''. Nature Phys 14, 447–450 (2018).
https://doi.org/10.1038/s41567-018-0048-5
[12] R. G. Melko, G. Carleo, J. Carrasquilla, and J. I. Cirac. ``Restricted boltzmann machines in quantum physics''. Nature Physics 15, 887–892 (2019).
https://doi.org/10.1038/s41567-019-0545-1
[13] J. Carrasquilla, G. Torlai, R. G. Melko, and L. Aolita. ``Reconstructing quantum states with generative models''. Nature Machine Intelligence 1, 155–161 (2019).
https://doi.org/10.1038/s42256-019-0028-1
[14] J. Carrasquilla and G. Torlai. ``How to use neural networks to investigate quantum many-body physics''. PRX Quantum 2, 040201 (2021).
https://doi.org/10.1103/PRXQuantum.2.040201
[15] Jing Chen, Song Cheng, Haidong Xie, Lei Wang, and Tao Xiang. ``Equivalence of restricted boltzmann machines and tensor network states''. Phys. Rev. B 97, 085104 (2018).
https://doi.org/10.1103/PhysRevB.97.085104
[16] U. Schollwoeck. ``The density-matrix renormalization group in the age of matrix product states''. Annals of Physics 326, 96–192 (2011).
https://doi.org/10.1016/j.aop.2010.09.012
[17] S. Morawetz, I. J. S. De Vlugt, and R. G. Carrasquilla, J.and Melko. ``U(1)-symmetric recurrent neural networks for quantum state reconstruction''. Physical Review A 104 (2021).
https://doi.org/10.1103/physreva.104.012401
[18] Mohamed Hibat-Allah, Martin Ganahl, Lauren E. Hayward, Roger G. Melko, and Juan Carrasquilla. ``Recurrent neural network wave functions''. Phys. Rev. Res. 2, 023358 (2020).
https://doi.org/10.1103/PhysRevResearch.2.023358
[19] Stefanie Czischek, M. Schuyler Moss, Matthew Radzihovsky, Ejaaz Merali, and Roger G. Melko. ``Data-enhanced variational monte carlo simulations for rydberg atom arrays''. Phys. Rev. B 105, 205108 (2022).
https://doi.org/10.1103/PhysRevB.105.205108
[20] A. Rocchetto, E. Grant, S. Strelchuk, G. Carleo, and S. Severini. ``Learning hard quantum distributions with variational autoencoders''. npj Quantum Information 4, 28 (2018).
https://doi.org/10.1038/s41534-018-0077-z
[21] Tobias Schmale, Moritz Reh, and Martin Gärttner. ``Efficient quantum state tomography with convolutional neural networks''. npj Quantum Information 8, 115 (2022).
https://doi.org/10.1038/s41534-022-00621-4
[22] S. Ahmed, C. Sánchez Muñoz, F. Nori, and A. F. Kockum. ``Quantum state tomography with conditional generative adversarial networks''. Phys. Rev. Lett. 127, 140502 (2021).
https://doi.org/10.1103/PhysRevLett.127.140502
[23] P. Cha, P. Ginsparg, F. Wu, J. Carrasquilla, P. L. McMahon, and E.-A. Kim. ``Attention-based quantum tomography''. Machine Learning: Science and Technology 3, 01LT01 (2021).
https://doi.org/10.1088/2632-2153/ac362b
[24] Yuan-Hang Zhang and Massimiliano Di Ventra. ``Transformer quantum state: A multipurpose model for quantum many-body problems''. Physical Review B 107 (2023).
https://doi.org/10.1103/physrevb.107.075147
[25] G. Torlai, B. Timar, E. P. L. van Nieuwenburg, H. Levine, A. Omran, A. Keesling, H. Bernien, M. Greiner, V. Vuletic, M. D. Lukin, R. G. Melko, and M. Endres. ``Integrating neural networks with a quantum simulator for state reconstruction''. Phys. Rev. Lett. 123, 230504 (2019).
https://doi.org/10.1103/PhysRevLett.123.230504
[26] B. Settles. ``Active learning literature survey''. Computer Sciences Technical Report (2009). url: burrsettles.com/pub/settles.activelearning.pdf.
https://burrsettles.com/pub/settles.activelearning.pdf
[27] R. Greiner, A. J. Grove, and D. Roth. ``Learning cost-sensitive active classifiers''. Artificial Intelligence 139, 137–174 (2002).
https://doi.org/10.1016/S0004-3702(02)00209-6
[28] S. Tong and E. Chang. ``Support vector machine active learning for image retrieval''. Proc. of the 9th ACM Intern. Conf. on MultimediaPage 107–118 (2001).
https://doi.org/10.1145/500141.500159
[29] G. Tur, D. Hakkani-Tür, and R. E. Schapire. ``Combining active and semi-supervised learning for spoken language understanding''. Speech Communication 45, 171–186 (2005).
https://doi.org/10.1016/j.specom.2004.08.002
[30] J. Yao, Y. Wu, J. Koo, B. Yan, and H. Zhai. ``Active learning algorithm for computational physics''. Phys. Rev. Research 2, 013287 (2020).
https://doi.org/10.1103/PhysRevResearch.2.013287
[31] Y. Ding, J. D. Martín-Guerrero, Y. Song, R. Magdalena-Benedicto, and X. Chen. ``Active learning for the optimal design of multinomial classification in physics''. Phys. Rev. Research 4, 013213 (2022).
https://doi.org/10.1103/PhysRevResearch.4.013213
[32] Y. Ding, J. D. Martín-Guerrero, M. Sanz, R. Magdalena-Benedicto, X. Chen, and E. Solano. ``Retrieving quantum information with active learning''. Phys. Rev. Lett. 124, 140504 (2020).
https://doi.org/10.1103/PhysRevLett.124.140504
[33] F. Huszár and N. M. T. Houlsby. ``Adaptive bayesian quantum tomography''. Phys. Rev. A 85, 052120 (2012).
https://doi.org/10.1103/PhysRevA.85.052120
[34] D. H. Mahler, L. A. Rozema, A. Darabi, C. Ferrie, R. Blume-Kohout, and A. M. Steinberg. ``Adaptive quantum state tomography improves accuracy quadratically''. Phys. Rev. Lett. 111, 183601 (2013).
https://doi.org/10.1103/PhysRevLett.111.183601
[35] C. Ferrie. ``Self-guided quantum tomography''. Phys. Rev. Lett. 113, 190404 (2014).
https://doi.org/10.1103/PhysRevLett.113.190404
[36] S. S. Straupe. ``Adaptive quantum tomography''. Jetp Lett. 104, 510–522 (2016).
https://doi.org/10.1134/S0021364016190024
[37] Y. Wu, Z. Meng, K. Wen, C. Mi, J. Zhang, and H. Zhai. ``Active learning approach to optimization of experimental control''. Chinese Physics Letters 37, 103201 (2020).
https://doi.org/10.1088/0256-307x/37/10/103201
[38] M. Cramer, M. B. Plenio, S. T. Flammia, R. Somma, D. Gross, S. D. Bartlett, O. Landon-Cardinal, D. Poulin, and Y.-K. Liu. ``Efficient quantum state tomography''. Nature Communications 1, 149 (2010).
https://doi.org/10.1038/ncomms1147
[39] M. J. S. Beach, I. De Vlugt, A. Golubeva, P. Huembeli, B. Kulchytskyy, X. Luo, R. G. Melko, E. Merali, and G. Torlai. ``QuCumber: wavefunction reconstruction with neural networks''. SciPost Phys. 7, 9 (2019).
https://doi.org/10.21468/SciPostPhys.7.1.009
[40] Xun Gao and Lu-Ming Duan. ``Efficient representation of quantum many-body states with deep neural networks''. Nature Communications 8, 2041–1723 (2017).
https://doi.org/10.1038/s41467-017-00705-2
[41] Giacomo Torlai and Roger G. Melko. ``Latent space purification via neural density operators''. Phys. Rev. Lett. 120, 240503 (2018).
https://doi.org/10.1103/PhysRevLett.120.240503
[42] Douglas Hendry, Hongwei Chen, and Adrian Feiguin. ``Neural network representation for minimally entangled typical thermal states''. Phys. Rev. B 106, 165111 (2022).
https://doi.org/10.1103/PhysRevB.106.165111
[43] Dan Sehayek, Anna Golubeva, Michael S. Albergo, Bohdan Kulchytskyy, Giacomo Torlai, and Roger G. Melko. ``Learnability scaling of quantum states: Restricted boltzmann machines''. Phys. Rev. B 100, 195125 (2019).
https://doi.org/10.1103/PhysRevB.100.195125
[44] ``Qucumber v1.3.2 documentation''. https://qucumber.readthedocs.io/en/stable/.
https://qucumber.readthedocs.io/en/stable/
[45] Yoav Freund, H. Sebastian Seung, Eli Shamir, and Naftali Tishby. ``Selective sampling using the query by committee algorithm''. Machine Learning 28, 1573–0565 (1997).
https://doi.org/10.1023/A:1007330508534
[46] H. S. Seung, M. Opper, and H. Sompolinsky. ``Query by committee''. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory. Page 287–294. COLT '92New York, NY, USA (1992). Association for Computing Machinery.
https://doi.org/10.1145/130385.130417
[47] Andrew McCallum and Kamal Nigam. ``Employing em and pool-based active learning for text classification''. In Proceedings of the Fifteenth International Conference on Machine Learning. Page 350–358. ICML 98San Francisco, CA, USA (1998). Morgan Kaufmann Publishers Inc.
[48] Fernando Pereira, Naftali Tishby, and Lillian Lee. ``Distributional clustering of English words''. In 31st Annual Meeting of the Association for Computational Linguistics. Pages 183–190. Columbus, Ohio, USA (1993). Association for Computational Linguistics.
https://doi.org/10.3115/981574.981598
[49] J.K Chung, P.L Kannappan, C.T Ng, and P.K Sahoo. ``Measures of distance between probability distributions''. Journal of Mathematical Analysis and Applications 138, 280–292 (1989).
https://doi.org/10.1016/0022-247X(89)90335-1
[50] ``$\mathrm{IBM}$ quantum website''. https://quantum-computing.ibm.com/.
https://quantum-computing.ibm.com/
[51] G. Aleksandrowicz, T. Alexander, P. Barkoutsos, L. Bello, Y. Ben-Haim, D. Bucher, F. J. Cabrera-Hernández, J. Carballo-Franquis, A. Chen, J.M. Chow, A.D. Córcoles-Gonzales, A. J Cross, A. Cross, J. Cruz-Benito, Culver C., and authors. ``Qiskit: An Open-source Framework for Quantum Computing''. Zenodo (2019).
https://doi.org/10.5281/zenodo.2562111
[52] C. Hubig, F. Lachenmaier, N.-O. Linden, T. Reinhard, L. Stenzel, A. Swoboda, and M. Grundner. ``The SyTen toolkit''.
[53] C. Hubig. ``Symmetry-protected tensor networks''. PhD thesis. LMU München. (2017). url: edoc.ub.uni-muenchen.de/21348/.
https://edoc.ub.uni-muenchen.de/21348/
[54] T. Iadecola and M. Schecter. ``Quantum many-body scar states with emergent kinetic constraints and finite-entanglement revivals''. Phys. Rev. B 101, 024306 (2020).
https://doi.org/10.1103/PhysRevB.101.024306
[55] U. Borla, R. Verresen, F. Grusdt, and S. Moroz. ``Confined phases of one-dimensional spinless fermions coupled to ${Z}_{2}$ gauge theory''. Phys. Rev. Lett. 124, 120503 (2020).
https://doi.org/10.1103/PhysRevLett.124.120503
[56] M. Kebrič, L. Barbiero, C. Reinmoser, U. Schollwöck, and F. Grusdt. ``Confinement and mott transitions of dynamical charges in one-dimensional lattice gauge theories''. Phys. Rev. Lett. 127, 167203 (2021).
https://doi.org/10.1103/PhysRevLett.127.167203
[57] A. J. Ferris and G. Vidal. ``Perfect sampling with unitary tensor networks''. Phys. Rev. B 85, 165146 (2012).
https://doi.org/10.1103/PhysRevB.85.165146
[58] Maximilian Buser, Ulrich Schollwöck, and Fabian Grusdt. ``Snapshot-based characterization of particle currents and the hall response in synthetic flux lattices''. Phys. Rev. A 105, 033303 (2022).
https://doi.org/10.1103/PhysRevA.105.033303
[59] G. Semeghini, H. Levine, A. Keesling, S. Ebadi, T. T. Wang, D. Bluvstein, R. Verresen, H. Pichler, M. Kalinowski, R. Samajdar, A. Omran, S. Sachdev, A. Vishwanath, M. Greiner, V. Vuletić, and authors. ``Probing topological spin liquids on a programmable quantum simulator''. Science 374, 1242–1247 (2021).
https://doi.org/10.1126/science.abi8794
[60] K. J. Satzinger, Y.-J Liu, A. Smith, C. Knapp, M. Newman, C. Jones, Z. Chen, C. Quintana, X. Mi, A. Dunsworth, C. Gidney, I. Aleiner, F. Arute, K. Arya, J. Atalaya, and authors. ``Realizing topologically ordered states on a quantum processor''. Science 374, 1237–1241 (2021).
https://doi.org/10.1126/science.abi8378
[61] H.-Y. Huang, R. Kueng, and J. Preskill. ``Predicting many properties of a quantum system from very few measurements''. Nature Physics 16, 1050–1057 (2020).
https://doi.org/10.1038/s41567-020-0932-7
[62] M. J. S. Beach, I. De Vlugt, A. Golubeva, P. Huembeli, B. Kulchytskyy, X. Luo, R. G. Melko, E. Merali, and G. Torlai. ``QuCumber: wavefunction reconstruction with neural networks''. SciPost Phys. 7, 9 (2019).
https://doi.org/10.21468/SciPostPhys.7.1.009
[63] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. ``Deep learning''. MIT Press. (2016). url: http://www.deeplearningbook.org.
http://www.deeplearningbook.org
[64] P. Mehta, M. Bukov, C. Wang, A. G.R. Day, C. Richardson, C. K. Fisher, and D. J. Schwab. ``A high-bias, low-variance introduction to machine learning for physicists''. Physics Reports 810, 1–124 (2019).
https://doi.org/10.1016/j.physrep.2019.03.001
[65] C. Prosko, S.-P. Lee, and J. Maciejko. ``Simple $\mathbb{Z}_{2}$ lattice gauge theories at finite fermion density''. Phys. Rev. B 96, 205104 (2017).
https://doi.org/10.1103/PhysRevB.96.205104
Cited by
[1] Daipengwei Bao, Min Liu, Yangwei Ou, Qingshan Xu, Qin Li, and Xiaoqing Tan, "Eigenvalue-based quantum state verification of three-qubit W class states", Physica A: Statistical Mechanics and its Applications 639, 129681 (2024).
[2] M. Schuyler Moss, Sepehr Ebadi, Tout T. Wang, Giulia Semeghini, Annabelle Bohrdt, Mikhail D. Lukin, and Roger G. Melko, "Enhancing variational Monte Carlo simulations using a programmable quantum simulator", Physical Review A 109 3, 032410 (2024).
[3] Abigail McClain Gomez, Susanne F. Yelin, and Khadijeh Najafi, "Reconstructing Quantum States Using Basis-Enhanced Born Machines", arXiv:2206.01273, (2022).
[4] Katherine Van Kirk, Jordan Cotler, Hsin-Yuan Huang, and Mikhail D. Lukin, "Hardware-efficient learning of quantum many-body states", arXiv:2212.06084, (2022).
[5] Matjaž Kebrič, Umberto Borla, Ulrich Schollwöck, Sergej Moroz, Luca Barbiero, and Fabian Grusdt, "Confinement induced frustration in a one-dimensional \mathbf{\mathbb{Z}_2} lattice gauge theory", New Journal of Physics 25 1, 013035 (2023).
[6] Ruidi Zhu, Ciara Pike-Burke, and Florian Mintert, "Active Learning for Quantum Mechanical Measurements", arXiv:2212.07513, (2022).
[7] Alexander Lidiak, Casey Jameson, Zhen Qin, Gongguo Tang, Michael B. Wakin, Zhihui Zhu, and Zhexuan Gong, "Quantum state tomography with tensor train cross approximation", arXiv:2207.06397, (2022).
[8] Yuxuan Du, Yibo Yang, Tongliang Liu, Zhouchen Lin, Bernard Ghanem, and Dacheng Tao, "ShadowNet for Data-Centric Quantum System Learning", arXiv:2308.11290, (2023).
[9] Yongcheng Ding, José D. Martín-Guerrero, Yolanda Vives-Gilabert, and Xi Chen, "Active Learning in Physics: From 101, to Progress, and Perspective", arXiv:2307.03899, (2023).
The above citations are from Crossref's cited-by service (last updated successfully 2024-05-13 06:59:37) and SAO/NASA ADS (last updated successfully 2024-05-13 06:59:38). The list may be incomplete as not all publishers provide suitable and complete citation data.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.