Operational Quantum Average-Case Distances
1Center for Theoretical Physics, Polish Academy of Sciences, Al. Lotników 32/46, 02-668 Warszawa, Poland
2Research Institute for Advanced Computer Science (RIACS), USRA, Moffett Field, CA
3Institute of Theoretical and Applied Informatics, Polish Academy of Sciences, 44-100 Gliwice, Poland
4Faculty of Physics, Astronomy and Applied Computer Science, Jagiellonian University, 30-348 Kraków, Poland
| Published: | 2023-09-11, volume 7, page 1106 |
| Eprint: | arXiv:2112.14283v5 |
| Doi: | https://doi.org/10.22331/q-2023-09-11-1106 |
| Citation: | Quantum 7, 1106 (2023). |
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
We introduce distance measures between quantum states, measurements, and channels based on their statistical distinguishability in generic experiments. Specifically, we analyze the average Total Variation Distance (TVD) between output statistics of protocols in which quantum objects are intertwined with random circuits and measured in standard basis. We show that for circuits forming approximate 4-designs, the average TVDs can be approximated by simple explicit functions of the underlying objects – the average-case distances (ACDs). We apply them to analyze the effects of noise in quantum advantage experiments and for efficient discrimination of high-dimensional states and channels without quantum memory. We argue that ACDs are better suited for assessing the quality of NISQ devices than common distance measures such as trace distance or the diamond norm.
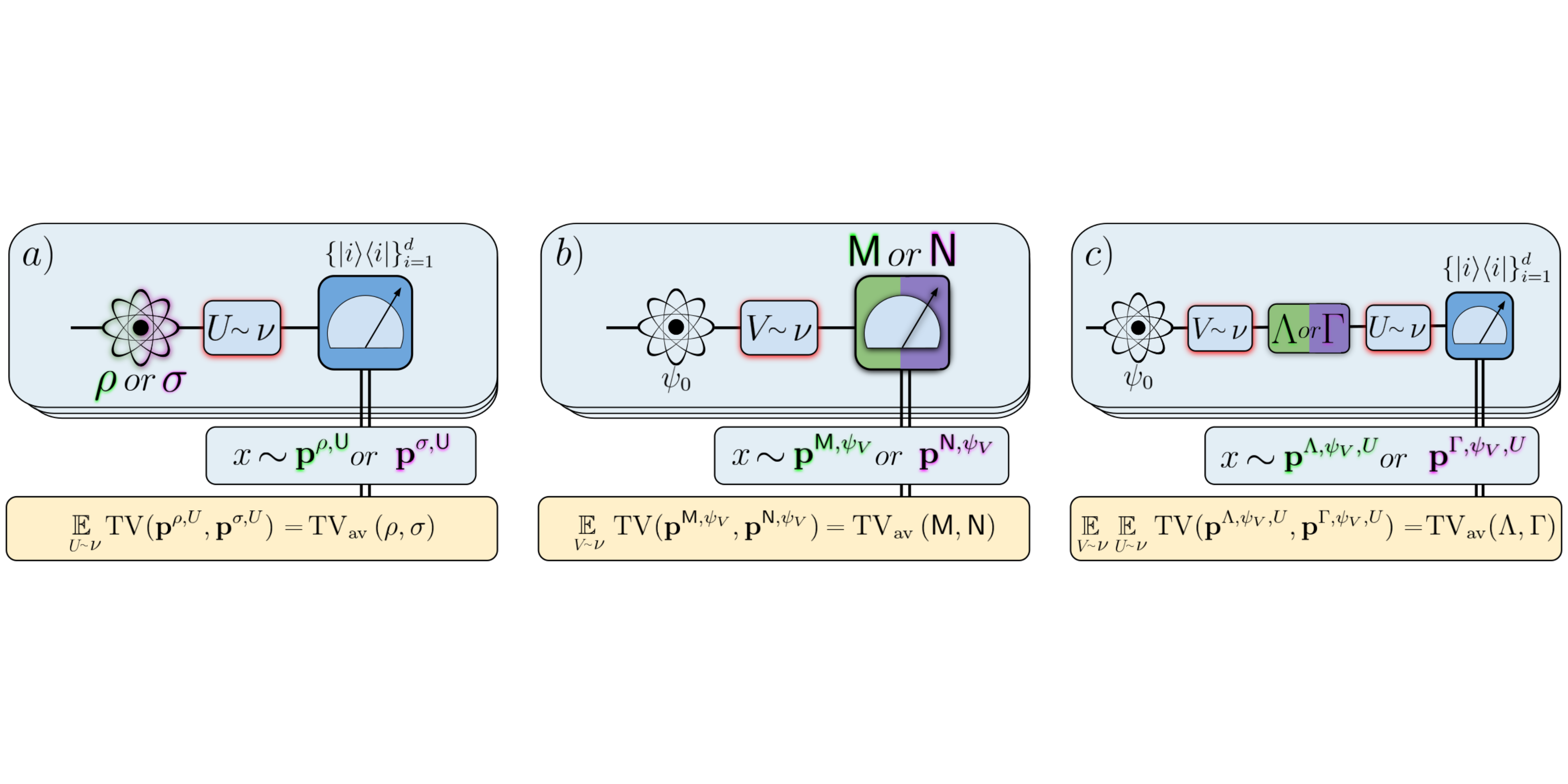
Featured image: Measures of the distance between quantum objects based on average statistical distinguishability. For quantum states a), we take the average over random unitaries applied to the state, followed by measurement in the standard basis. For quantum measurements b), we take the average over random pure states measured on the detector. Finally, for quantum channels c) we take the average over independent random unitaries applied before and after the application of the channel.
Popular summary
We apply AC distances to evaluate the impact of noise on quantum advantage protocols based on random circuit sampling. AC distances provide both lower and upper bounds for average total variation, helping to quantify how far noisy outputs stray from ideal or become trivially uniform. For instance, we show that even in the absence of gate and state-preparation noise, the local, symmetric bitflip error in measurements causes noisy distribution to approach trivial one exponentially quickly in system size.
Our findings also extend to randomized quantum algorithms. AC distances can efficiently quantify the distinguishability of quantum objects using simple, local random circuits. We study two scenarios related to those recently analyzed in the context of so-called Quantum Algorithmic Measurement and complexity growth of quantum circuits: (i) distinguishing Haar random N qubit pure state from maximally mixed state and (ii) distinguishing N qubit Haar random unitary from maximally depolarizing channel. Our findings imply that protocols employing random circuits can be used to efficiently discriminate quantum objects. Since they do not depend on the objects to be distinguished, randomized measurement schemes can be interpreted as "universal discriminators", analogous to the SWAP test but not requiring the usage of entanglement or coherent access to copies of quantum systems.
► BibTeX data
► References
[1] Scott Aaronson. Shadow tomography of quantum states. SIAM Journal on Computing, 49(5):STOC18–368–STOC18–394, 2020. doi:10.1137/18M120275X.
https://doi.org/10.1137/18M120275X
[2] Dorit Aharonov, Jordan Cotler, and Xiao-Liang Qi. Quantum algorithmic measurement. Nature Communications, 13(1), feb 2022. doi:10.1038/s41467-021-27922-0.
https://doi.org/10.1038/s41467-021-27922-0
[3] Andris Ambainis and Joseph Emerson. Quantum T-designs: T-wise independence in the quantum world. In Proceedings of the Twenty-Second Annual IEEE Conference on Computational Complexity, CCC '07, page 129–140, USA, 2007. IEEE Computer Society. doi:10.1109/CCC.2007.26.
https://doi.org/10.1109/CCC.2007.26
[4] MD SAJID ANIS et al. Qiskit: An open-source framework for quantum computing, 2021. doi:10.5281/zenodo.2573505.
https://doi.org/10.5281/zenodo.2573505
[5] Frank Arute et al. Quantum supremacy using a programmable superconducting processor. Nature, 574(7779):505–510, 10 2019. doi:10.1038/s41586-019-1666-5.
https://doi.org/10.1038/s41586-019-1666-5
[6] Ingemar Bengtsson and Karol Zyczkowski. Geometry of Quantum States: An Introduction to Quantum Entanglement. Cambridge University Press, 2006. doi:10.1017/CBO9780511535048.
https://doi.org/10.1017/CBO9780511535048
[7] Bonnie Berger. The fourth moment method. SIAM Journal on Computing, 26(4):1188–1207, 1997. doi:10.1137/S0097539792240005.
https://doi.org/10.1137/S0097539792240005
[8] Sergio Boixo, Sergei V. Isakov, Vadim N. Smelyanskiy, Ryan Babbush, Nan Ding, Zhang Jiang, Michael J. Bremner, John M. Martinis, and Hartmut Neven. Characterizing quantum supremacy in near-term devices. Nature Physics, 14(6):595–600, 6 2018. doi:10.1038/s41567-018-0124-x.
https://doi.org/10.1038/s41567-018-0124-x
[9] Fernando G. S. L. Brandão, Aram W. Harrow, and Michał Horodecki. Local random quantum circuits are approximate polynomial-designs. Communications in Mathematical Physics, 346(2):397–434, 9 2016. doi:10.1007/s00220-016-2706-8.
https://doi.org/10.1007/s00220-016-2706-8
[10] Fernando G.S.L. Brandão, Wissam Chemissany, Nicholas Hunter-Jones, Richard Kueng, and John Preskill. Models of quantum complexity growth. PRX Quantum, 2:030316, 7 2021. doi:10.1103/PRXQuantum.2.030316.
https://doi.org/10.1103/PRXQuantum.2.030316
[11] Senrui Chen, Wenjun Yu, Pei Zeng, and Steven T. Flammia. Robust shadow estimation. PRX Quantum, 2(3), 9 2021. doi:10.1103/prxquantum.2.030348.
https://doi.org/10.1103/prxquantum.2.030348
[12] Joseph Emerson, Robert Alicki, and Karol Życzkowski. Scalable noise estimation with random unitary operators. Journal of Optics B: Quantum and Semiclassical Optics, 7(10):S347–S352, 9 2005. doi:10.1088/1464-4266/7/10/021.
https://doi.org/10.1088/1464-4266/7/10/021
[13] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. A quantum approximate optimization algorithm, 2014. arXiv:1411.4028.
arXiv:1411.4028
[14] Edward Farhi and Aram W Harrow. Quantum supremacy through the quantum approximate optimization algorithm, 2019. arXiv:1602.07674.
arXiv:1602.07674
[15] Steven T. Flammia. Averaged circuit eigenvalue sampling, 2021. arXiv:2108.05803.
arXiv:2108.05803
[16] Jay M. Gambetta, A. D. Córcoles, S. T. Merkel, B. R. Johnson, John A. Smolin, Jerry M. Chow, Colm A. Ryan, Chad Rigetti, S. Poletto, Thomas A. Ohki, and et al. Characterization of addressability by simultaneous randomized benchmarking. Physical Review Letters, 109(24), 12 2012. doi:10.1103/physrevlett.109.240504.
https://doi.org/10.1103/physrevlett.109.240504
[17] Guillermo García-Pérez, Matteo A.C. Rossi, Boris Sokolov, Francesco Tacchino, Panagiotis Kl. Barkoutsos, Guglielmo Mazzola, Ivano Tavernelli, and Sabrina Maniscalco. Learning to measure: Adaptive informationally complete generalized measurements for quantum algorithms. PRX Quantum, 2(4), 11 2021. doi:10.1103/prxquantum.2.040342.
https://doi.org/10.1103/prxquantum.2.040342
[18] Alexei Gilchrist, Nathan K. Langford, and Michael A. Nielsen. Distance measures to compare real and ideal quantum processes. Phys. Rev. A, 71(6):062310, 6 2005. doi:10.1103/PhysRevA.71.062310.
https://doi.org/10.1103/PhysRevA.71.062310
[19] Charles Hadfield. Adaptive pauli shadows for energy estimation, 2021. arXiv:2105.12207.
arXiv:2105.12207
[20] Charles Hadfield, Sergey Bravyi, Rudy Raymond, and Antonio Mezzacapo. Measurements of quantum hamiltonians with locally-biased classical shadows. Communications in Mathematical Physics, 391(3):951–967, May 2022. doi:10.1007/s00220-022-04343-8.
https://doi.org/10.1007/s00220-022-04343-8
[21] Jonas Haferkamp and Nicholas Hunter-Jones. Improved spectral gaps for random quantum circuits: Large local dimensions and all-to-all interactions. Phys. Rev. A, 104:022417, 8 2021. doi:10.1103/PhysRevA.104.022417.
https://doi.org/10.1103/PhysRevA.104.022417
[22] Pierre Hansen and Brigitte Jaumard. Algorithms for the maximum satisfiability problem. Computing, 44(4):279–303, 12 1990. doi:10.1007/BF02241270.
https://doi.org/10.1007/BF02241270
[23] Matthew P. Harrigan et al. Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nature Physics, 17(3):332–336, feb 2021. doi:10.1038/s41567-020-01105-y.
https://doi.org/10.1038/s41567-020-01105-y
[24] Aram W. Harrow. The church of the symmetric subspace, 2013. arXiv:1308.6595.
arXiv:1308.6595
[25] Aram W. Harrow and Saeed Mehraban. Approximate unitary t-designs by short random quantum circuits using nearest-neighbor and long-range gates. Communications in Mathematical Physics, 401(2):1531–1626, may 2023. doi:10.1007/s00220-023-04675-z.
https://doi.org/10.1007/s00220-023-04675-z
[26] Jonas Helsen, Xiao Xue, Lieven M. K. Vandersypen, and Stephanie Wehner. A new class of efficient randomized benchmarking protocols. npj Quantum Information, 5(1):71, Aug 2019. doi:10.1038/s41534-019-0182-7.
https://doi.org/10.1038/s41534-019-0182-7
[27] Eric Huang, Andrew C. Doherty, and Steven Flammia. Performance of quantum error correction with coherent errors. Phys. Rev. A, 99(2):022313, 2 2019. doi:10.1103/PhysRevA.99.022313.
https://doi.org/10.1103/PhysRevA.99.022313
[28] Hsin-Yuan Huang, Richard Kueng, and John Preskill. Predicting many properties of a quantum system from very few measurements. Nature Physics, 16(10):1050–1057, 6 2020. doi:10.1038/s41567-020-0932-7.
https://doi.org/10.1038/s41567-020-0932-7
[29] Hsin-Yuan Huang, Richard Kueng, and John Preskill. Information-theoretic bounds on quantum advantage in machine learning. Phys. Rev. Lett., 126(19):190505, 5 2021. doi:10.1103/PhysRevLett.126.190505.
https://doi.org/10.1103/PhysRevLett.126.190505
[30] J. L. W. V. Jensen. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Mathematica, 30(none):175 – 193, 1906. doi:10.1007/BF02418571.
https://doi.org/10.1007/BF02418571
[31] J. R. Johansson, P. D. Nation, and Franco Nori. QuTiP: An open-source python framework for the dynamics of open quantum systems. Computer Physics Communications, 183(8):1760–1772, 2012. doi:https://doi.org/10.1016/j.cpc.2012.02.021.
https://doi.org/10.1016/j.cpc.2012.02.021
[32] J. R. Johansson, P. D. Nation, and Franco Nori. QuTiP 2: A python framework for the dynamics of open quantum systems. Computer Physics Communications, 184(4):1234–1240, 2013. doi:https://doi.org/10.1016/j.cpc.2012.11.019.
https://doi.org/10.1016/j.cpc.2012.11.019
[33] Abhinav Kandala, Antonio Mezzacapo, Kristan Temme, Maika Takita, Markus Brink, Jerry M. Chow, and Jay M. Gambetta. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature, 549(7671):242–246, sep 2017. doi:10.1038/nature23879.
https://doi.org/10.1038/nature23879
[34] Richard Kueng, Huangjun Zhu, and David Gross. Distinguishing quantum states using clifford orbits. arXiv e-prints, 9 2016. arXiv:1609.08595.
arXiv:1609.08595
[35] J. S. Lundeen, A. Feito, H. Coldenstrodt-Ronge, K. L. Pregnell, Ch. Silberhorn, T. C. Ralph, J. Eisert, M. B. Plenio, and I. A. Walmsley. Tomography of quantum detectors. Nature Physics, 5:27, 11 2008. doi:10.1038/nphys1133.
https://doi.org/10.1038/nphys1133
[36] Filip B. Maciejewski, Flavio Baccari, Zoltán Zimborás, and Michał Oszmaniec. Modeling and mitigation of cross-talk effects in readout noise with applications to the quantum approximate optimization algorithm. Quantum, 5:464, 6 2021. doi:10.22331/q-2021-06-01-464.
https://doi.org/10.22331/q-2021-06-01-464
[37] Filip B. Maciejewski, Zbigniew Puchała, and Michał Oszmaniec. Exploring quantum average-case distances: Proofs, properties, and examples. IEEE Transactions on Information Theory, 69(7):4600–4619, 2023. doi:10.1109/TIT.2023.3250100.
https://doi.org/10.1109/TIT.2023.3250100
[38] Filip B. Maciejewski, Zoltán Zimborás, and Michał Oszmaniec. Mitigation of readout noise in near-term quantum devices by classical post-processing based on detector tomography. Quantum, 4:257, 4 2020. doi:10.22331/q-2020-04-24-257.
https://doi.org/10.22331/q-2020-04-24-257
[39] Easwar Magesan, J. M. Gambetta, and Joseph Emerson. Scalable and robust randomized benchmarking of quantum processes. Physical Review Letters, 106(18), 5 2011. doi:10.1103/physrevlett.106.180504.
https://doi.org/10.1103/physrevlett.106.180504
[40] Easwar Magesan, Jay M. Gambetta, B. R. Johnson, Colm A. Ryan, Jerry M. Chow, Seth T. Merkel, Marcus P. da Silva, George A. Keefe, Mary B. Rothwell, Thomas A. Ohki, and et al. Efficient measurement of quantum gate error by interleaved randomized benchmarking. Physical Review Letters, 109(8), 8 2012. doi:10.1103/physrevlett.109.080505.
https://doi.org/10.1103/physrevlett.109.080505
[41] Jarrod R. McClean, Sergio Boixo, Vadim N. Smelyanskiy, Ryan Babbush, and Hartmut Neven. Barren plateaus in quantum neural network training landscapes. Nature Communications, 9:4812, 11 2018. doi:10.1038/s41467-018-07090-4.
https://doi.org/10.1038/s41467-018-07090-4
[42] Miguel Navascués and Sandu Popescu. How energy conservation limits our measurements. Phys. Rev. Lett., 112:140502, 4 2014. doi:10.1103/PhysRevLett.112.140502.
https://doi.org/10.1103/PhysRevLett.112.140502
[43] Michael A. Nielsen and Isaac L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press, 2010. doi:10.1017/CBO9780511976667.
https://doi.org/10.1017/CBO9780511976667
[44] Michał Oszmaniec, Leonardo Guerini, Peter Wittek, and Antonio Acín. Simulating positive-operator-valued measures with projective measurements. Phys. Rev. Lett., 119:190501, 11 2017. doi:10.1103/PhysRevLett.119.190501.
https://doi.org/10.1103/PhysRevLett.119.190501
[45] Michał Oszmaniec, Adam Sawicki, and Michał Horodecki. Epsilon-nets, unitary designs and random quantum circuits. IEEE Transactions on Information Theory, pages 1–1, 2021. doi:10.1109/TIT.2021.3128110.
https://doi.org/10.1109/TIT.2021.3128110
[46] Robert M. Parrish, Edward G. Hohenstein, Peter L. McMahon, and Todd J. Martínez. Quantum computation of electronic transitions using a variational quantum eigensolver. Phys. Rev. Lett., 122:230401, 6 2019. doi:10.1103/PhysRevLett.122.230401.
https://doi.org/10.1103/PhysRevLett.122.230401
[47] Alberto Peruzzo, Jarrod McClean, Peter Shadbolt, Man-Hong Yung, Xiao-Qi Zhou, Peter J. Love, Alán Aspuru-Guzik, and Jeremy L. O’Brien. A variational eigenvalue solver on a photonic quantum processor. Nature Communications, 5(1), 7 2014. doi:10.1038/ncomms5213.
https://doi.org/10.1038/ncomms5213
[48] John Preskill. Quantum Computing in the NISQ era and beyond. Quantum, 2:79, 8 2018. doi:10.22331/q-2018-08-06-79.
https://doi.org/10.22331/q-2018-08-06-79
[49] Zbigniew Puchała, Łukasz Pawela, Aleksandra Krawiec, and Ryszard Kukulski. Strategies for optimal single-shot discrimination of quantum measurements. Physical Review A, 98(4), 10 2018. doi:10.1103/physreva.98.042103.
https://doi.org/10.1103/physreva.98.042103
[50] John Watrous. Semidefinite programs for completely bounded norms. Theory of Computing, 5(11):217–238, 2009. doi:10.4086/toc.2009.v005a011.
https://doi.org/10.4086/toc.2009.v005a011
[51] Qingling Zhu et al. Quantum computational advantage via 60-qubit 24-cycle random circuit sampling. Science Bulletin, 67(3):240–245, 2022. doi:10.1016/j.scib.2021.10.017.
https://doi.org/10.1016/j.scib.2021.10.017
Cited by
[1] Giacomo De Palma and Dario Trevisan, "The Wasserstein Distance of Order 1 for Quantum Spin Systems on Infinite Lattices", Annales Henri Poincaré 24 12, 4237 (2023).
[2] E. A. Pankovets and L. E. Fedichkin, "Metric on the Space of Quantum Processes", Proceedings of the Steklov Institute of Mathematics 324 1, 169 (2024).
[3] Michał Oszmaniec, Marcin Kotowski, Michał Horodecki, and Nicholas Hunter-Jones, "Saturation and recurrence of quantum complexity in random local quantum dynamics", arXiv:2205.09734, (2022).
[4] Filip B. Maciejewski, Zbigniew Puchała, and Michał Oszmaniec, "Exploring Quantum Average-Case Distances: proofs, properties, and examples", arXiv:2112.14284, (2021).
The above citations are from Crossref's cited-by service (last updated successfully 2024-07-26 21:32:35) and SAO/NASA ADS (last updated successfully 2024-07-26 21:32:35). The list may be incomplete as not all publishers provide suitable and complete citation data.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.