Real-Time Krylov Theory for Quantum Computing Algorithms

Yizhi Shen; Katherine Klymko; James Sud; David B. Williams-Young; Wibe A. de Jong; Norm M. Tubman

doi:10.22331/q-2023-07-25-1066

Real-Time Krylov Theory for Quantum Computing Algorithms

Yizhi Shen^1,2,3, Katherine Klymko⁴, James Sud^1,5, David B. Williams-Young⁶, Wibe A. de Jong⁶, and Norm M. Tubman¹

¹NASA Ames Research Center, Moffett Field, CA 94035, USA
²KBR, 601 Jefferson St., Houston, TX 77002
³Department of Chemistry, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
⁴NERSC, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
⁵USRA Research Institute for Advanced Computer Science, Mountain View, CA 94043, USA
⁶Applied Mathematics and Computational Research Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA

Published:	2023-07-25, volume 7, page 1066
Eprint:	arXiv:2208.01063v3
Doi:	https://doi.org/10.22331/q-2023-07-25-1066
Citation:	Quantum 7, 1066 (2023).

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

Quantum computers provide new avenues to access ground and excited state properties of systems otherwise difficult to simulate on classical hardware. New approaches using subspaces generated by real-time evolution have shown efficiency in extracting eigenstate information, but the full capabilities of such approaches are still not understood. In recent work, we developed the variational quantum phase estimation (VQPE) method, a compact and efficient real-time algorithm to extract eigenvalues on quantum hardware. Here we build on that work by theoretically and numerically exploring a generalized Krylov scheme where the Krylov subspace is constructed through a parametrized real-time evolution, which applies to the VQPE algorithm as well as others. We establish an error bound that justifies the fast convergence of our spectral approximation. We also derive how the overlap with high energy eigenstates becomes suppressed from real-time subspace diagonalization and we visualize the process that shows the signature phase cancellations at specific eigenenergies. We investigate various algorithm implementations and consider performance when stochasticity is added to the target Hamiltonian in the form of spectral statistics. To demonstrate the practicality of such real-time evolution, we discuss its application to fundamental problems in quantum computation such as electronic structure predictions for strongly correlated systems.

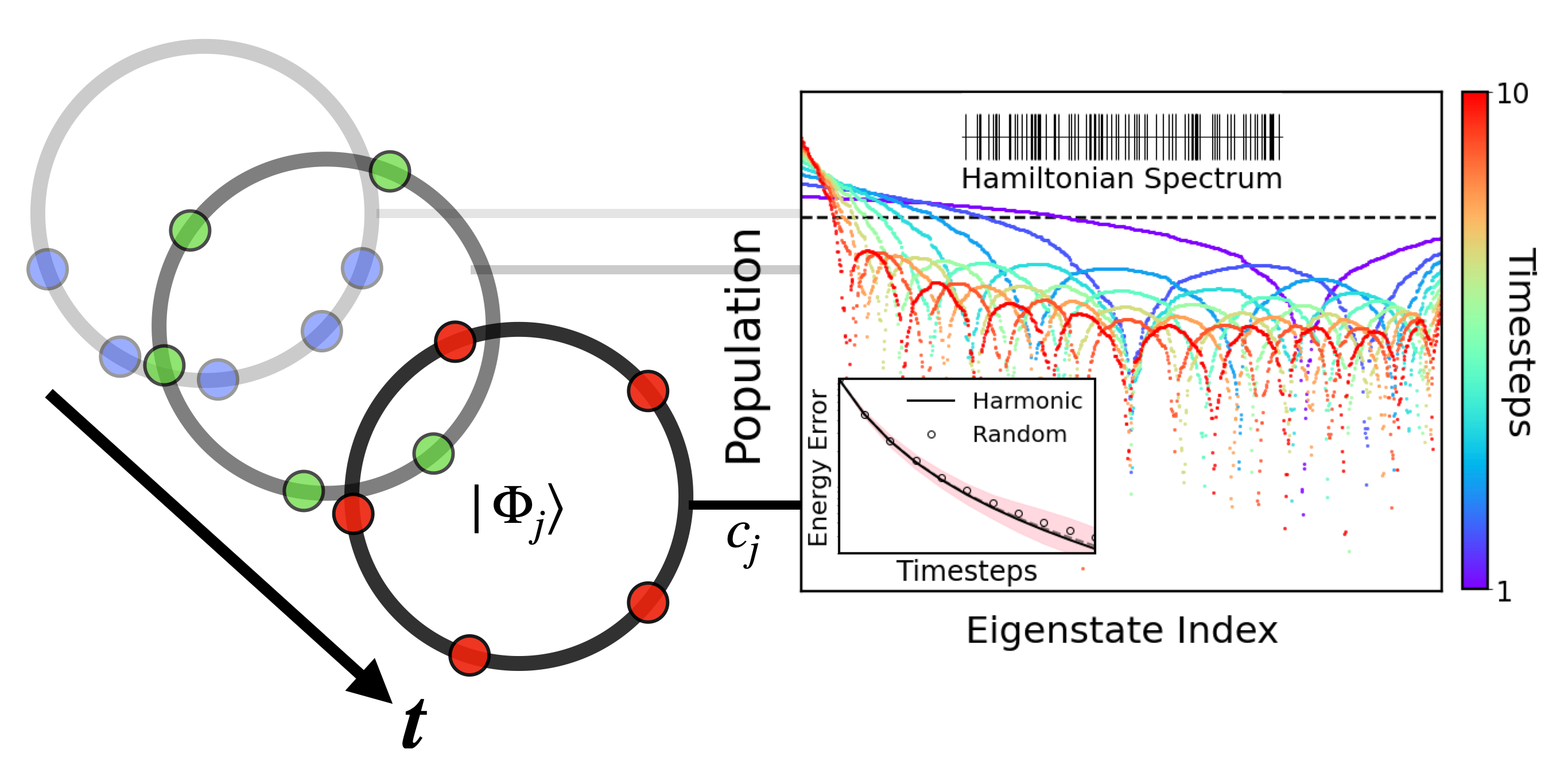
Popular summary

Near-term approaches exploiting quantum dynamics have shown great promise in extracting eigenstate information, but the full capabilities of such approaches are still not understood. In this work, we make a timely step forward in understanding their properties by exploring and analyzing a generalized Krylov subspace scheme where the subspace is constructed from a parametrized real-time evolution. We establish an error bound on the spectral convergence, and derive how the overlap with high energy eigenstates becomes rapidly suppressed. In addition, we investigate various algorithmic implementations and consider performance when stochasticity is added to the target Hamiltonian. To demonstrate the practical edge of such real-time methods, we discuss fundamental problems in quantum computation such as electronic structure predictions on strongly correlated materials, highlighting the encouraging efficacy.

► BibTeX data

@article{Shen2023realtimekrylov,
  doi = {10.22331/q-2023-07-25-1066},
  url = {https://doi.org/10.22331/q-2023-07-25-1066},
  title = {Real-{T}ime {K}rylov {T}heory for {Q}uantum {C}omputing {A}lgorithms},
  author = {Shen, Yizhi and Klymko, Katherine and Sud, James and Williams-Young, David B. and Jong, Wibe A. de and Tubman, Norm M.},
  journal = {{Quantum}},
  issn = {2521-327X},
  publisher = {{Verein zur F{\"{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}},
  volume = {7},
  pages = {1066},
  month = jul,
  year = {2023}
}

► References

[1] Bela Bauer, Dave Wecker, Andrew J. Millis, Matthew B. Hastings, and Matthias Troyer. Hybrid quantum-classical approach to correlated materials. Phys. Rev. X, 6: 031045, Sep 2016. https://doi.org/10.1103/PhysRevX.6.031045.
https://doi.org/10.1103/PhysRevX.6.031045

[2] Jun Li, Xiaodong Yang, Xinhua Peng, and Chang-Pu Sun. Hybrid quantum-classical approach to quantum optimal control. Phys. Rev. Lett., 118: 150503, Apr 2017. https://doi.org/10.1103/PhysRevLett.118.150503.
https://doi.org/10.1103/PhysRevLett.118.150503

[3] D. Zhu, N. M. Linke, M. Benedetti, K. A. Landsman, N. H. Nguyen, C. H. Alderete, A. Perdomo-Ortiz, N. Korda, A. Garfoot, C. Brecque, L. Egan, O. Perdomo, and C. Monroe. Training of quantum circuits on a hybrid quantum computer. Science Advances, 5 (10): eaaw9918, 2019. https://doi.org/10.1126/sciadv.aaw9918.
https://doi.org/10.1126/sciadv.aaw9918

[4] Jarrod R McClean, Mollie E Kimchi-Schwartz, Jonathan Carter, and Wibe A De Jong. Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states. Phys. Rev. A, 95 (4): 042308, 2017. https://doi.org/10.1103/PhysRevA.95.042308.
https://doi.org/10.1103/PhysRevA.95.042308

[5] Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C Bardin, Rami Barends, Rupak Biswas, Sergio Boixo, Fernando GSL Brandao, David A Buell, et al. Quantum supremacy using a programmable superconducting processor. Nature, 574 (7779): 505–510, 2019. https://doi.org/10.1038/s41586-019-1666-5.
https://doi.org/10.1038/s41586-019-1666-5

[6] Sam McArdle, Suguru Endo, Alan Aspuru-Guzik, Simon C Benjamin, and Xiao Yuan. Quantum computational chemistry. Reviews of Modern Physics, 92 (1): 015003, 2020. https://doi.org/10.1103/RevModPhys.92.015003.
https://doi.org/10.1103/RevModPhys.92.015003

[7] Lin Lin and Yu Tong. Heisenberg-limited ground-state energy estimation for early fault-tolerant quantum computers. PRX Quantum, 3: 010318, Feb 2022. 10.1103/PRXQuantum.3.010318.
https://doi.org/10.1103/PRXQuantum.3.010318

[8] Dong An, Di Fang, and Lin Lin. Time-dependent unbounded Hamiltonian simulation with vector norm scaling. Quantum, 5: 459, May 2021. ISSN 2521-327X. https://doi.org/10.22331/q-2021-05-26-459.
https://doi.org/10.22331/q-2021-05-26-459

[9] Yu Tong, Dong An, Nathan Wiebe, and Lin Lin. Fast inversion, preconditioned quantum linear system solvers, fast green's-function computation, and fast evaluation of matrix functions. Phys. Rev. A, 104: 032422, Sep 2021. https://doi.org/10.1103/PhysRevA.104.032422.
https://doi.org/10.1103/PhysRevA.104.032422

[10] Yudong Cao, Jonathan Romero, Jonathan P. Olson, Matthias Degroote, Peter D. Johnson, Mária Kieferová, Ian D. Kivlichan, Tim Menke, Borja Peropadre, Nicolas P. D. Sawaya, Sukin Sim, Libor Veis, and Alán Aspuru-Guzik. Quantum chemistry in the age of quantum computing. Chemical Reviews, 119 (19): 10856–10915, 2019. https://doi.org/10.1021/acs.chemrev.8b00803.
https://doi.org/10.1021/acs.chemrev.8b00803

[11] Bela Bauer, Sergey Bravyi, Mario Motta, and Garnet Kin-Lic Chan. Quantum algorithms for quantum chemistry and quantum materials science. Chemical Reviews, 120 (22): 12685–12717, 2020. https://doi.org/10.1021/acs.chemrev.9b00829.
https://doi.org/10.1021/acs.chemrev.9b00829

[12] Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C Bardin, Rami Barends, Andreas Bengtsson, Sergio Boixo, Michael Broughton, Bob B Buckley, et al. Observation of separated dynamics of charge and spin in the fermi-hubbard model. arXiv preprint arXiv:2010.07965, 2020a. https://doi.org/10.48550/arXiv.2010.07965.
https://doi.org/10.48550/arXiv.2010.07965
arXiv:2010.07965

[13] Michael A. Nielsen and Isaac L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press, 2010. https://doi.org/10.1017/CBO9780511976667.
https://doi.org/10.1017/CBO9780511976667

[14] Alberto Peruzzo, Jarrod R. McClean, Peter J Shadbolt, Man-Hong Yung, Xiao-Qi Zhou, Peter J. Love, Alán Aspuru-Guzik, and Jeremy Lloyd O'Brien. A variational eigenvalue solver on a photonic quantum processor. Nature Communications, 5, 2014. https://doi.org/10.1038/ncomms5213.
https://doi.org/10.1038/ncomms5213

[15] Dave Wecker, Matthew B Hastings, and Matthias Troyer. Progress towards practical quantum variational algorithms. Physical Review A, 92 (4): 042303, 2015. https://doi.org/10.1103/PhysRevA.92.042303.
https://doi.org/10.1103/PhysRevA.92.042303

[16] Kevin J Sung, Jiahao Yao, Matthew P Harrigan, Nicholas C Rubin, Zhang Jiang, Lin Lin, Ryan Babbush, and Jarrod R McClean. Using models to improve optimizers for variational quantum algorithms. Quantum Science and Technology, 5 (4): 044008, sep 2020. https://doi.org/10.1088/2058-9565/abb6d9.
https://doi.org/10.1088/2058-9565/abb6d9

[17] William James Huggins, Joonho Lee, Unpil Baek, Bryan O'Gorman, and K Birgitta Whaley. A non-orthogonal variational quantum eigensolver. New J. Phys., 2020. https://doi.org/10.1088/1367-2630/ab867b.
https://doi.org/10.1088/1367-2630/ab867b

[18] Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C Bardin, Rami Barends, Sergio Boixo, Michael Broughton, Bob B Buckley, David A Buell, et al. Hartree-fock on a superconducting qubit quantum computer. Science, 369 (6507): 1084–1089, 2020b. https://doi.org/10.1126/science.abb9811.
https://doi.org/10.1126/science.abb9811

[19] Dmitry A. Fedorov, Bo Peng, Niranjan Govind, and Yuri Alexeev. VQE method: a short survey and recent developments. Materials Theory, 6 (1): 2, Jan 2022. https://doi.org/10.1186/s41313-021-00032-6.
https://doi.org/10.1186/s41313-021-00032-6

[20] Jarrod R McClean, Jonathan Romero, Ryan Babbush, and Alán Aspuru-Guzik. The theory of variational hybrid quantum-classical algorithms. New Journal of Physics, 18 (2): 023023, feb 2016. https://doi.org/10.1088/1367-2630/18/2/023023.
https://doi.org/10.1088/1367-2630/18/2/023023

[21] Tyler Takeshita, Nicholas C Rubin, Zhang Jiang, Eunseok Lee, Ryan Babbush, and Jarrod R McClean. Increasing the representation accuracy of quantum simulations of chemistry without extra quantum resources. Phys. Rev. X, 10 (1): 011004, 2020. https://doi.org/10.1103/PhysRevX.10.011004.
https://doi.org/10.1103/PhysRevX.10.011004

[22] Robert M Parrish, Edward G Hohenstein, Peter L McMahon, and Todd J Martínez. Quantum computation of electronic transitions using a variational quantum eigensolver. Physical review letters, 122 (23): 230401, 2019. https://doi.org/10.1103/PhysRevLett.122.230401.
https://doi.org/10.1103/PhysRevLett.122.230401

[23] Miroslav Urbanek, Daan Camps, Roel Van Beeumen, and Wibe A de Jong. Chemistry on quantum computers with virtual quantum subspace expansion. J. Chem. Theory Comput., 16 (9): 5425, 2020. https://doi.org/10.1021/acs.jctc.0c00447.
https://doi.org/10.1021/acs.jctc.0c00447

[24] Nicholas H Stair, Renke Huang, and Francesco A Evangelista. A multireference quantum krylov algorithm for strongly correlated electrons. J. Chem. Theory Comput., 16 (4): 2236–2245, 2020. https://doi.org/10.1021/acs.jctc.9b01125.
https://doi.org/10.1021/acs.jctc.9b01125

[25] Cristian L. Cortes and Stephen K. Gray. Quantum krylov subspace algorithms for ground- and excited-state energy estimation. Phys. Rev. A, 105: 022417, Feb 2022. https://doi.org/10.1103/PhysRevA.105.022417.
https://doi.org/10.1103/PhysRevA.105.022417

[26] Katherine Klymko, Carlos Mejuto-Zaera, Stephen J Cotton, Filip A. Wudarski, Miroslav Urbánek, Diptarka Hait, Martin Head-Gordon, K. Birgitta Whaley, Jonathan Edward Moussa, Nathan Wiebe, Wibe A. de Jong, and Norm M. Tubman. Real-time evolution for ultracompact hamiltonian eigenstates on quantum hardware. PRX Quantum, 3 (020323), 2022. https://doi.org/10.1103/PRXQuantum.3.020323.
https://doi.org/10.1103/PRXQuantum.3.020323

[27] Tae Jun Park and JC Light. Unitary quantum time evolution by iterative lanczos reduction. The Journal of chemical physics, 85 (10): 5870–5876, 1986. https://doi.org/10.1063/1.451548.
https://doi.org/10.1063/1.451548

[28] Daniel Neuhauser. Bound state eigenfunctions from wave packets: Time→ energy resolution. The Journal of chemical physics, 93 (4): 2611–2616, 1990. https://doi.org/10.1063/1.458900.
https://doi.org/10.1063/1.458900

[29] Daniel Neuhauser. Circumventing the heisenberg principle: A rigorous demonstration of filter-diagonalization on a licn model. The Journal of chemical physics, 100 (7): 5076–5079, 1994. https://doi.org/10.1063/1.467224.
https://doi.org/10.1063/1.467224

[30] Michael R Wall and Daniel Neuhauser. Extraction, through filter-diagonalization, of general quantum eigenvalues or classical normal mode frequencies from a small number of residues or a short-time segment of a signal. i. theory and application to a quantum-dynamics model. The Journal of chemical physics, 102 (20): 8011–8022, 1995. https://doi.org/10.1063/1.468999.
https://doi.org/10.1063/1.468999

[31] Cornelius Lanczos. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. Journal of research of the National Bureau of Standards, 45: 255–282, 1950. https://doi.org/10.6028/jres.045.026.
https://doi.org/10.6028/jres.045.026

[32] B.N. Parlett. The Symmetric Eigenvalue Problem. Classics in Applied Mathematics. Society for Industrial and Applied Mathematics, 1980. ISBN 9780898714029. https://doi.org/10.1137/1.9781611971163.
https://doi.org/10.1137/1.9781611971163

[33] H. D. Meyer and S. Pal. A band-lanczos method for computing matrix elements of a resolvent. J. Chem. Phys., 91: 6195, 1989. https://doi.org/10.1063/1.457438.
https://doi.org/10.1063/1.457438

[34] Salvatore R Manmana, Alejandro Muramatsu, and Reinhard M Noack. Time evolution of one-dimensional quantum many body systems. In AIP Conference Proceedings, volume 789, pages 269–278. American Institute of Physics, 2005. https://doi.org/10.1063/1.2080353.
https://doi.org/10.1063/1.2080353

[35] E. Pavarini, E. Koch, D. Vollhardt, and A. Lichtenstein, editors. The LDA+DMFT approach to strongly correlated materials, chapter 8, pages 235–264. Verlag des Forschungszentrum Jülich, 2011. ISBN 978-3-89336-734-4.

[36] R. V. Mises and H. Pollaczek-Geiringer. Praktische verfahren der gleichungsauflösung. ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, 9 (2): 152–164, 1929. https://doi.org/10.1002/zamm.19290090206.
https://doi.org/10.1002/zamm.19290090206

[37] Mario Motta, Chong Sun, Adrian TK Tan, Matthew J O`Rourke, Erika Ye, Austin J Minnich, Fernando GSL Brandao, and Garnet Kin Lic Chan. Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution. Nature Physics, 16 (2): 205–210, 2020. https://doi.org/10.1038/s41567-019-0704-4.
https://doi.org/10.1038/s41567-019-0704-4

[38] Kübra Yeter-Aydeniz, Raphael C Pooser, and George Siopsis. Practical quantum computation of chemical and nuclear energy levels using quantum imaginary time evolution and lanczos algorithms. npj Quantum Information, 6 (1): 1–8, 2020. https://doi.org/10.1038/s41534-020-00290-1.
https://doi.org/10.1038/s41534-020-00290-1

[39] William J Huggins, Bryan A O’Gorman, Nicholas C Rubin, David R Reichman, Ryan Babbush, and Joonho Lee. Unbiasing fermionic quantum monte carlo with a quantum computer. Nature, 603 (7901): 416–420, 2022. https://doi.org/10.1038/s41586-021-04351-z.
https://doi.org/10.1038/s41586-021-04351-z

[40] Lov K. Grover. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, STOC '96, page 212–219, New York, NY, USA, 1996. Association for Computing Machinery. ISBN 0897917855. https://doi.org/10.1145/237814.237866.
https://doi.org/10.1145/237814.237866

[41] Andrew M. Childs and Nathan Wiebe. Hamiltonian simulation using linear combinations of unitary operations. Quantum Info. Comput., 12 (11–12): 901–924, nov 2012. ISSN 1533-7146. https://doi.org/10.26421/QIC12.11-12-1.
https://doi.org/10.26421/QIC12.11-12-1

[42] Desmond J Higham and Nicholas J Higham. Structured backward error and condition of generalized eigenvalue problems. SIAM Journal on Matrix Analysis and Applications, 20 (2): 493–512, 1998. https://doi.org/10.1137/S0895479896313188.
https://doi.org/10.1137/S0895479896313188

[43] Christopher C. Paige. The computation of eigenvalues and eigenvectors of very large sparse matrices. 1971.

[44] Y. Saad. On the rates of convergence of the lanczos and the block-lanczos methods. SIAM Journal on Numerical Analysis, 17 (5): 687–706, 1980. ISSN 00361429. https://doi.org/10.1137/0717059.
https://doi.org/10.1137/0717059

[45] Ethan N. Epperly, Lin Lin, and Yuji Nakatsukasa. A theory of quantum subspace diagonalization. SIAM Journal on Matrix Analysis and Applications, 43 (3): 1263–1290, 2022. https://doi.org/10.1137/21M145954X.
https://doi.org/10.1137/21M145954X

[46] Christine Schmid and Kyle J. DeMars. Angular correlation using rogers-szegő-chaos. Mathematics, 8 (2), 2020. ISSN 2227-7390. https://doi.org/10.3390/math8020171.
https://doi.org/10.3390/math8020171

[47] Mama Foupouagnigni and Wolfram Koepf. Orthogonal Polynomials: 2nd AIMS-Volkswagen Stiftung Workshop, Douala, Cameroon, 5-12 October, 2018. 01 2020. ISBN 978-3-030-36743-5. https://doi.org/10.1007/978-3-030-36744-2.
https://doi.org/10.1007/978-3-030-36744-2

[48] Roger A Horn and Charles R Johnson. Matrix analysis. Cambridge university press, 2012. https://doi.org/10.1017/CBO9780511810817.
https://doi.org/10.1017/CBO9780511810817

[49] Florian Weigend and Reinhart Ahlrichs. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for h to rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys., 7: 3297, 2005. 10.1039/b508541a.
https://doi.org/10.1039/b508541a

[50] Norm M. Tubman, Joonho Lee, Tyler Y. Takeshita, Martin Head-Gordon, and K. Birgitta Whaley. A deterministic alternative to the full configuration interaction quantum monte carlo method. J. Chem. Phys., 145 (4): 044112, 2016. https://doi.org/10.1063/1.4955109.
https://doi.org/10.1063/1.4955109

[51] Norm M Tubman, Daniel S Levine, Diptarka Hait, Martin Head-Gordon, and K Birgitta Whaley. An efficient deterministic perturbation theory for selected configuration interaction methods. arXiv preprint arXiv:1808.02049v1, 2018. https://doi.org/10.48550/arXiv.1808.02049.
https://doi.org/10.48550/arXiv.1808.02049
arXiv:1808.02049v1

[52] Norm M Tubman, C Daniel Freeman, Daniel S Levine, Diptarka Hait, Martin Head-Gordon, and K Birgitta Whaley. Modern approaches to exact diagonalization and selected configuration interaction with the adaptive sampling ci method. Journal of chemical theory and computation, 16 (4): 2139–2159, 2020. https://doi.org/10.1021/acs.jctc.8b00536.
https://doi.org/10.1021/acs.jctc.8b00536

[53] Robert M Parrish and Peter L McMahon. Quantum filter diagonalization: Quantum eigendecomposition without full quantum phase estimation. arXiv preprint arXiv:1909.08925, 2019. https://doi.org/10.48550/arXiv.1909.08925.
https://doi.org/10.48550/arXiv.1909.08925
arXiv:1909.08925

[54] Yulong Dong, Lin Lin, and Yu Tong. Ground-state preparation and energy estimation on early fault-tolerant quantum computers via quantum eigenvalue transformation of unitary matrices. PRX Quantum, 3: 040305, Oct 2022. https://doi.org/10.1103/PRXQuantum.3.040305.
https://doi.org/10.1103/PRXQuantum.3.040305

[55] Peter W Atkins and Ronald S Friedman. Molecular quantum mechanics, 5th edition. Oxford university press, 2011. https://doi.org/10.1080/00107514.2012.678277.
https://doi.org/10.1080/00107514.2012.678277

[56] P.A. Absil, R. Mahony, and R. Sepulchre. Optimization Algorithms on Matrix Manifolds. Princeton University Press, 2009. ISBN 9781400830244. https://doi.org/10.1515/9781400830244.
https://doi.org/10.1515/9781400830244

[57] Nguyen Thanh Son, P.-A. Absil, Bin Gao, and Tatjana Stykel. Computing symplectic eigenpairs of symmetric positive-definite matrices via trace minimization and riemannian optimization. SIAM Journal on Matrix Analysis and Applications, 42 (4): 1732–1757, 2021. https://doi.org/10.1137/21M1390621.
https://doi.org/10.1137/21M1390621

[58] C. G. Baker, P.-A. Absil, and K. A. Gallivan. An implicit Riemannian trust-region method for the symmetric generalized eigenproblem. In Computational Science – ICCS 2006, volume 3991 of LNCS, pages 210–217. Springer, 2006. https://doi.org/10.1007/11758501_32.
https://doi.org/10.1007/11758501_32

[59] Jérémie Roland and Nicolas J. Cerf. Noise resistance of adiabatic quantum computation using random matrix theory. Phys. Rev. A, 71: 032330, Mar 2005. https://doi.org/10.1103/PhysRevA.71.032330.
https://doi.org/10.1103/PhysRevA.71.032330

[60] Siddharth Muthukrishnan, Tameem Albash, and Daniel A. Lidar. Sensitivity of quantum speedup by quantum annealing to a noisy oracle. Phys. Rev. A, 99: 032324, Mar 2019. https://doi.org/10.1103/PhysRevA.99.032324.
https://doi.org/10.1103/PhysRevA.99.032324

Cited by

[1] Chukwudubem Umeano, François Jamet, Lachlan P. Lindoy, Ivan Rungger, and Oleksandr Kyriienko, "Quantum subspace expansion approach for simulating dynamical response functions of Kitaev spin liquids", Physical Review Materials 9 3, 034401 (2025).

[2] Refaat Ismail, I-Chi Chen, Chen Zhao, Ronen Weiss, Fangli Liu, Hengyun Zhou, Sheng-Tao Wang, Andrew Sornborger, and Milan Kornjača, "Transversal Architecture for Megaquop-Scale Quantum Simulation with Neutral Atoms", PRX Quantum 7 2, 020343 (2026).

[3] Lewis W. Anderson, Martin Kiffner, Tom O'Leary, Jason Crain, and Dieter Jaksch, "Solving lattice gauge theories using the quantum Krylov algorithm and qubitization", Quantum 9, 1669 (2025).

[4] Antonios M. Alvertis, Abid Khan, Thomas Iadecola, Peter P. Orth, and Norm Tubman, "Classical Benchmarks for Variational Quantum Eigensolver Simulations of the Hubbard Model", Quantum 9, 1748 (2025).

[5] Gastón F. Scialchi, Augusto J. Roncaglia, and Diego A. Wisniacki, "Integrability-to-chaos transition through the Krylov approach for state evolution", Physical Review E 109 5, 054209 (2024).

[6] Yijin Mao and Yuwen Zhang, "Modeling Heat Conduction With an Internal Heat Source Using a Quantum Lattice Boltzmann Method", ASME Journal of Heat and Mass Transfer 148 2, 021403 (2026).

[7] Aaron Szasz, Ed Younis, and Wibe Albert de Jong, "Ground state energy and magnetization curve of a frustrated magnetic system from real-time evolution on a digital quantum processor", Quantum 9, 1704 (2025).

[8] Gwonhak Lee, Dongkeun Lee, and Joonsuk Huh, "Sampling Error Analysis in Quantum Krylov Subspace Diagonalization", Quantum 8, 1477 (2024).

[9] William Kirby, "Analysis of quantum Krylov algorithms with errors", Quantum 8, 1457 (2024).

[10] Yizhi Shen, Daan Camps, Aaron Szasz, Siva Darbha, Katherine Klymko, David B. Williams--Young, Norm M. Tubman, and Roel Van Beeumen, "Estimating Eigenenergies from Quantum Dynamics: A Unified Noise-Resilient Measurement-Driven Approach", Quantum 9, 1836 (2025).

[11] Anjali A. Agrawal, João C. Getelina, Akhil Francis, and A. F. Kemper, "Cheaper and more noise-resilient quantum state preparation using eigenvector continuation", Physical Review A 111 3, 032607 (2025).

[12] Erik Lötstedt and Tamás Szidarovszky, "Rovibrational energy levels of H2O by quantum computing", The Journal of Chemical Physics 165 2, 024118 (2026).

[13] Ruyu Yang, Tianren Wang, Bing-Nan Lu, Ying Li, and Xiaosi Xu, "Shadow-based quantum subspace algorithm for the nuclear shell model", Physical Review A 111 1, 012620 (2025).

[14] Erik J. Gustafson, Juha Tiihonen, Diana Chamaki, Farshud Sorourifar, J. Wayne Mullinax, Andy C. Y. Li, Filip B. Maciejewski, Nicolas P. D. Sawaya, Jaron T. Krogel, David E. Bernal Neira, and Norm M. Tubman, "Surrogate optimization of variational quantum circuits", Proceedings of the National Academy of Sciences 122 36, e2408530122 (2025).

[15] Zongkang Zhang, Anbang Wang, Xiaosi Xu, and Ying Li, "Measurement-efficient quantum Krylov subspace diagonalisation", Quantum 8, 1438 (2024).

[16] Nobuyuki Yoshioka, Mirko Amico, William Kirby, Petar Jurcevic, Arkopal Dutt, Bryce Fuller, Shelly Garion, Holger Haas, Ikko Hamamura, Alexander Ivrii, Ritajit Majumdar, Zlatko Minev, Mario Motta, Bibek Pokharel, Pedro Rivero, Kunal Sharma, Christopher J. Wood, Ali Javadi-Abhari, and Antonio Mezzacapo, "Krylov diagonalization of large many-body Hamiltonians on a quantum processor", Nature Communications 16 1, 5014 (2025).

[17] Yizhi Shen, Alex Buzali, Hong-Ye Hu, Katherine Klymko, Daan Camps, Susanne F. Yelin, and Roel Van Beeumen, "Efficient Measurement-Driven Eigenenergy Estimation with Classical Shadows", PRX Quantum 7 1, 010328 (2026).

[18] Gian Gentinetta, Friederike Metz, William Kirby, and Giuseppe Carleo, "Quantum finite-temperature Lanczos method", Physical Review Research 8 2, 023285 (2026).

[19] Mark R. Hirsbrunner, J. Wayne Mullinax, Yizhi Shen, David B. Williams-Young, Katherine Klymko, Roel Van Beeumen, and Norm M. Tubman, "A circuit-generated quantum subspace algorithm for the variational quantum eigensolver", The Journal of Chemical Physics 161 16, 164103 (2024).

[20] Hamzat A. Akande, Alexandre Perrin, Bruno Senjean, and Matthieu Saubanère, "Variational quantum subspace construction via symmetry-preserving cost functions", Physical Review A 112 3, 032623 (2025).

[21] S. Paeckel, "Spectral Decomposition and High-Accuracy Green’s Functions: Overcoming the Nyquist-Shannon Limit via Complex-time Krylov Expansion", Physical Review Letters 136 16, 160401 (2026).

[22] María Laura Olivera-Atencio, Jesús Casado-Pascual, and Denis Lacroix, "Exploring fixed points and eigenstates of quantum systems with reinforcement learning", Physical Review Research 8 3, 033087 (2026).

[23] Yizhi Shen, Daan Camps, Aaron Szasz, Siva Darbha, Katherine Klymko, David B. Williams-Young, Norm M. Tubman, and Roel Van Beeumen, 2023 IEEE International Conference on Quantum Computing and Engineering (QCE) 302 (2023) ISBN:979-8-3503-4323-6.

[24] Ruhee D'Cunha, Cristian L. Cortes, Laura Gagliardi, and Stephen K. Gray, "Fragment-based initialization for quantum subspace methods", Physical Review A 110 4, 042613 (2024).

[25] Laia Domingo, F. Borondo, Gastón Scialchi, Augusto J. Roncaglia, Gabriel G. Carlo, and Diego A. Wisniacki, "Quantum reservoir complexity by the Krylov evolution approach", Physical Review A 110 2, 022446 (2024).

[26] Daniel Marti-Dafcik, Hugh G. A. Burton, and David P. Tew, "Spin coupling is all you need: Encoding strong electron correlation in molecules on quantum computers", Physical Review Research 7 1, 013191 (2025).

[27] Stefano Rizzello, Michele Scaraggi, Andrew D. Nelson, Leonardo Primavera, Gaetano Napoli, Guglielmo Stecca, Raffaele Vitolo, and Samuele De Bartolo, "Multiscaling behavior of braided channel networks: An alternative formulation of Taylor's law variate transformations", Physical Review E 109 3, 034306 (2024).

[28] Hardeep Bassi, Yizhi Shen, Harish S. Bhat, and Roel Van Beeumen, "From noisy observables to accurate ground-state energies: A quantum–classical signal subspace approach with denoising", APL Quantum 2 4, 046103 (2025).

[29] Mario Motta, William Kirby, Ieva Liepuoniute, Kevin J Sung, Jeffrey Cohn, Antonio Mezzacapo, Katherine Klymko, Nam Nguyen, Nobuyuki Yoshioka, and Julia E Rice, "Subspace methods for electronic structure simulations on quantum computers", Electronic Structure 6 1, 013001 (2024).

[30] Yuri Alexeev, Maximilian Amsler, Marco Antonio Barroca, Sanzio Bassini, Torey Battelle, Daan Camps, David Casanova, Young Jay Choi, Frederic T. Chong, Charles Chung, Christopher Codella, Antonio D. Córcoles, James Cruise, Alberto Di Meglio, Ivan Duran, Thomas Eckl, Sophia Economou, Stephan Eidenbenz, Bruce Elmegreen, Clyde Fare, Ismael Faro, Cristina Sanz Fernández, Rodrigo Neumann Barros Ferreira, Keisuke Fuji, Bryce Fuller, Laura Gagliardi, Giulia Galli, Jennifer R. Glick, Isacco Gobbi, Pranav Gokhale, Salvador de la Puente Gonzalez, Johannes Greiner, Bill Gropp, Michele Grossi, Emanuel Gull, Burns Healy, Matthew R. Hermes, Benchen Huang, Travis S. Humble, Nobuyasu Ito, Artur F. Izmaylov, Ali Javadi-Abhari, Douglas Jennewein, Shantenu Jha, Liang Jiang, Barbara Jones, Wibe Albert de Jong, Petar Jurcevic, William Kirby, Stefan Kister, Masahiro Kitagawa, Joel Klassen, Katherine Klymko, Kwangwon Koh, Masaaki Kondo, Dog̃a Murat Kürkçüog̃lu, Krzysztof Kurowski, Teodoro Laino, Ryan Landfield, Matt Leininger, Vicente Leyton-Ortega, Ang Li, Meifeng Lin, Junyu Liu, Nicolas Lorente, Andre Luckow, Simon Martiel, Francisco Martin-Fernandez, Margaret Martonosi, Claire Marvinney, Arcesio Castaneda Medina, Dirk Merten, Antonio Mezzacapo, Kristel Michielsen, Abhishek Mitra, Tushar Mittal, Kyungsun Moon, Joel Moore, Sarah Mostame, Mario Motta, Young-Hye Na, Yunseong Nam, Prineha Narang, Yu-ya Ohnishi, Daniele Ottaviani, Matthew Otten, Scott Pakin, Vincent R. Pascuzzi, Edwin Pednault, Tomasz Piontek, Jed Pitera, Patrick Rall, Gokul Subramanian Ravi, Niall Robertson, Matteo A.C. Rossi, Piotr Rydlichowski, Hoon Ryu, Georgy Samsonidze, Mitsuhisa Sato, Nishant Saurabh, Vidushi Sharma, Kunal Sharma, Soyoung Shin, George Slessman, Mathias Steiner, Iskandar Sitdikov, In-Saeng Suh, Eric D. Switzer, Wei Tang, Joel Thompson, Synge Todo, Minh C. Tran, Dimitar Trenev, Christian Trott, Huan-Hsin Tseng, Norm M. Tubman, Esin Tureci, David García Valiñas, Sofia Vallecorsa, Christopher Wever, Konrad Wojciechowski, Xiaodi Wu, Shinjae Yoo, Nobuyuki Yoshioka, Victor Wen-zhe Yu, Seiji Yunoki, Sergiy Zhuk, and Dmitry Zubarev, "Quantum-centric supercomputing for materials science: A perspective on challenges and future directions", Future Generation Computer Systems 160, 666 (2024).

[31] Yuchen Wang and David A. Mazziotti, "Electronic excited states from a variance-based contracted quantum eigensolver", Physical Review A 108 2, 022814 (2023).

[32] Lewis W. Anderson, Martin Kiffner, Tom O'Leary, Jason Crain, and Dieter Jaksch, "Solving lattice gauge theories using the quantum Krylov algorithm and qubitization", arXiv:2403.08859, (2024).

[33] Emil Otis Rosanowski, Jurek Eisinger, Lena Funcke, Ulrich Poschinger, and Ferdinand Schmidt-Kaler, "Sample-Based Krylov Quantum Diagonalization for the Schwinger Model on Trapped-Ion and Superconducting Quantum Processors", arXiv:2510.26951, (2025).

[34] Carlos Mejuto-Zaera and Alexander F. Kemper, "Quantum eigenvector continuation for chemistry applications", Electronic Structure 5 4, 045007 (2023).

[35] Akhil Francis, Anjali A. Agrawal, Jack H. Howard, Efekan Kökcü, and A. F. Kemper, "Subspace Diagonalization on Quantum Computers using Eigenvector Continuation", arXiv:2209.10571, (2022).

[36] Amanda Bowman, "Nuclear Spectra from Quantum Lanczos Algorithm with Real-Time Evolution and Multiple Reference States", arXiv:2309.00759, (2023).

[37] Nicholas H. Stair, Cristian L. Cortes, Robert M. Parrish, Jeffrey Cohn, and Mario Motta, "Stochastic quantum Krylov protocol with double-factorized Hamiltonians", Physical Review A 107 3, 032414 (2023).

The above citations are from Crossref's cited-by service (last updated successfully 2026-08-10 15:13:05) and SAO/NASA ADS (last updated successfully 2026-08-10 15:13:07). The list may be incomplete as not all publishers provide suitable and complete citation data.

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.