Robust measurement of wave function topology on NISQ quantum computers

Xiao Xiao; J. K. Freericks; A. F. Kemper

doi:10.22331/q-2023-04-27-987

Robust measurement of wave function topology on NISQ quantum computers

Xiao Xiao¹, J. K. Freericks², and A. F. Kemper¹

¹Department of Physics, North Carolina State University, Raleigh, North Carolina 27695, USA
²Department of Physics, Georgetown University, 37th and O Sts. NW, Washington, DC 20057 USA

Published:	2023-04-27, volume 7, page 987
Eprint:	arXiv:2101.07283v6
Doi:	https://doi.org/10.22331/q-2023-04-27-987
Citation:	Quantum 7, 987 (2023).

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

Topological quantum phases of quantum materials are defined through their topological invariants. These topological invariants are quantities that characterize the global geometrical properties of the quantum wave functions and thus are immune to local noise. Here, we present a strategy to measure topological invariants on quantum computers. We show that our strategy can be easily integrated with the variational quantum eigensolver (VQE) so that the topological properties of generic quantum many-body states can be characterized on current quantum hardware. We demonstrate the robust nature of the method by measuring topological invariants for both non-interacting and interacting models, and map out interacting quantum phase diagrams on quantum simulators and IBM quantum hardware.

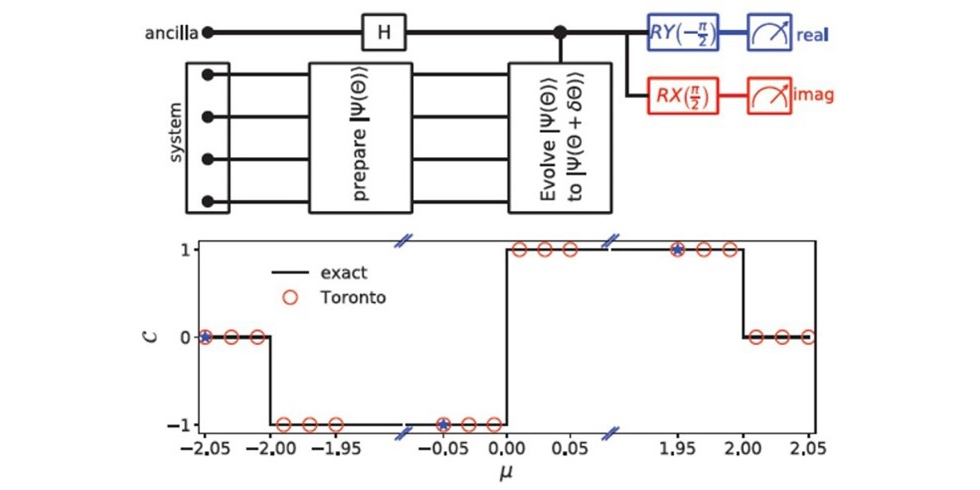
Featured image: A generic strategy allows accurate calculations of Chern numbers on IBM's quantum computers.

Popular summary

Calculations on current noisy intermediate-scale quantum (NISQ) hardware are susceptible to operation errors during the implementations of quantum circuits. Therefore, it is challenging to identify useful applications on which the present quantum hardware can be used. Here we provide a systematical strategy, which can be easily integrated with variational quantum algorithms, to characterize a key property of quantum matter: the wave function. Strikingly, we demonstrated that one important quantity that characterizes the wave function topology, the Chern number, can be calculated accurately on present quantum hardware without any error mitigation or error correction. Our work is an appealing demonstration that NISQ hardware might be a good platform to study quantum topological states and topological phenomena.

► BibTeX data

@article{Xiao2023robustmeasurementof,
  doi = {10.22331/q-2023-04-27-987},
  url = {https://doi.org/10.22331/q-2023-04-27-987},
  title = {Robust measurement of wave function topology on {NISQ} quantum computers},
  author = {Xiao, Xiao and Freericks, J. K. and Kemper, A. F.},
  journal = {{Quantum}},
  issn = {2521-327X},
  publisher = {{Verein zur F{\"{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}},
  volume = {7},
  pages = {987},
  month = apr,
  year = {2023}
}

► References

[1] D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, Phys. Rev. Lett. 49, 405 (1982).
https://doi.org/10.1103/PhysRevLett.49.405

[2] Q. Niu, D. J. Thouless, and Y.-S. Wu, Phys. Rev. B 31, 3372 (1985).
https://doi.org/10.1103/PhysRevB.31.3372

[3] D. N. Sheng, L. Sheng, and Z. Y. Weng, Phys. Rev. B 73, 233406 (2006).
https://doi.org/10.1103/PhysRevB.73.233406

[4] H. Obuse, A. Furusaki, S. Ryu, and C. Mudry, Phys. Rev. B 76, 075301 (2007).
https://doi.org/10.1103/PhysRevB.76.075301

[5] J. Li, R.-L. Chu, J. K. Jain, and S.-Q. Shen, Phys. Rev. Lett. 102, 136806 (2009).
https://doi.org/10.1103/PhysRevLett.102.136806

[6] E. Prodan, J. Phys. A: Math. Theor. 44, 113001 (2011).
https://doi.org/10.1088/1751-8113/44/11/113001

[7] J. T. Chalker, M. Ortuno, and A. M. Somoza, Phys. Rev. B 83, 115317 (2011).
https://doi.org/10.1103/PhysRevB.83.115317

[8] J. Liu, A. C. Potter, K. T. Law, and P. A. Lee, Phys. Rev. Lett. 109, 267002 (2012).
https://doi.org/10.1103/PhysRevLett.109.267002

[9] A. M. Lobos, R. M. Lutchyn, and S. Das Sarma, Phys. Rev. Lett. 109, 146403 (2012).
https://doi.org/10.1103/PhysRevLett.109.146403

[10] E. J. Konig, P. M. Ostrovsky, I. V. Protopopov, I. V. Gornyi, I. S. Burmistrov, and A. D. Mirlin Phys. Rev. B 88, 035106 (2013).
https://doi.org/10.1103/PhysRevB.88.035106

[11] A. Altland, D. Bagrets, L. Fritz, A. Kamenev, and H. Schmiedt, Phys. Rev. Lett. 112, 206602 (2014).
https://doi.org/10.1103/PhysRevLett.112.206602

[12] I. Mondragon-Shem, T. L. Hughes, J. Song, and E. Prodan, Phys. Rev. Lett. 113, 046802 (2014).
https://doi.org/10.1103/PhysRevLett.113.046802

[13] J. Song, and E. Prodan, Phys. Rev. B 89, 224203 (2014).
https://doi.org/10.1103/PhysRevB.89.224203

[14] M. S. Foster, H.-Y. Xie, and Y.-Z. Chou, Phys. Rev. B 89, 155140 (2014).
https://doi.org/10.1103/PhysRevB.89.155140

[15] J. Wang, B. Lian, and S.-C. Zhang, Phys. Rev. B 89, 085106 (2014).
https://doi.org/10.1103/PhysRevB.89.085106

[16] C. Liu, W. Gao, B. Yang, and S. Zhang, Phys. Rev. Lett. 119, 183901 (2017).
https://doi.org/10.1103/PhysRevLett.119.183901

[17] E. J. Meier, F. A. An, A. Dauphin, M. Maffei, P. Massignan, T. L. Hughes, B. Gadway, Science 362, 929 (2018).
https://doi.org/10.1126/science.aat3406

[18] S. Stutzer, Y. Plotnik, Y. Lumer, P. Titum, N. Linder, M. Segev, M. C. Rechtsman, and A. Szameit, Nature 560, 461 (2018).
https://doi.org/10.1038/s41586-018-0418-2

[19] X. Xiao, arXiv:1802.02687 (2018).
https://doi.org/10.48550/arXiv.1802.02687
arXiv:1802.02687

[20] O. Shtanko, and R. Movassagh, Phys. Rev. Lett. 121, 126803 (2018).
https://doi.org/10.1103/PhysRevLett.121.126803

[21] T. Okugawa, P. Tang, A. Rubio, and D. M. Kennes, Phys. Rev. B 102, 201405(R) (2020).
https://doi.org/10.1103/PhysRevB.102.201405

[22] P. Roushan, C. Neill, Yu Chen, M. Kolodrubetz, C. Quintana, N. Leung, M. Fang, R. Barends, B. Campbell, Z. Chen, B. Chiaro, A. Dunsworth, E. Jeffrey, J. Kelly, A. Megrant, J. Mutus, P. J. J. O’Malley, D. Sank, A. Vainsencher, J. Wenner, T. White, A. Polkovnikov, A. N. Cleland and J. M. Martinis Nature 515, 241 (2014).
https://doi.org/10.1038/nature13891

[23] K. Choo, C. W. von Keyserlingk, N. Regnault, and T. Neupert, Phys. Rev. Lett. 121, 086808 (2018).
https://doi.org/10.1103/PhysRevLett.121.086808

[24] A. Smith, B. Jobst, A. G. Green, and F. Pollmann, Phys. Rev. Research 4, L022020 (2022).
https://doi.org/10.1103/PhysRevResearch.4.L022020

[25] D. Azses, R. Haenel, Y. Naveh, R. Raussendorf, E. Sela, and E. G. DallaTorre, Phys. Rev. Lett. 125, 120502 (2020).
https://doi.org/10.1103/PhysRevLett.125.120502

[26] F. Mei, Q. Guo, Y.-F. Yu, L. Xiao, S.-L. Zhu, and S. Jia, Phys. Rev. Lett. 125, 160503 (2020).
https://doi.org/10.1103/PhysRevLett.125.160503

[27] X. Xiao, J. K. Freericks, and A. F. Kemper, Quantum 5, 553 (2021).
https://doi.org/10.22331/q-2021-09-28-553

[28] E. Flurin, V. V. Ramasesh, S. Hacohen-Gourgy, L. S. Martin, N. Y. Yao, and I. Siddiqi, Phys. Rev. X 7, 031023 (2017).
https://doi.org/10.1103/PhysRevX.7.031023

[29] X. Zhan, L. Xiao, Z. Bian, K. Wang, X. Qiu, B. C. Sanders, W. Yi, and P. Xue, Phys. Rev. Lett. 119, 130501 (2017).
https://doi.org/10.1103/PhysRevLett.119.130501

[30] X.-Y. Xu, Q.-Q. Wang, W.-W. Pan, K. Sun, J.-S. Xu, G. Chen, J.-S. Tang, M. Gong, Y.-J. Han, C.-F. Li, and G.-C. Guo, Phys. Rev. Lett. 120, 260501 (2018).
https://doi.org/10.1103/PhysRevLett.120.260501

[31] A. Elben, J. Yu, G. Zhu, M. Hafezi, F. Pollmann, P. Zoller, and B. Vermersch, Sci. Adv. 6, eaaz3666 (2020).
https://doi.org/10.1126/sciadv.aaz3666

[32] J. Preskill, Quantum 2, 79 (2018).
https://doi.org/10.22331/q-2018-08-06-79

[33] A. Kandala, K. Temme, A. D. Corcoles, A. Mezzacapo, J. M. Chow, and J. M. Gambetta, Nature 567, 491 (2019).
https://doi.org/10.1038/s41586-019-1040-7

[34] K. E. Hamilton, and R. C. Pooser, Quantum Machine Intelligence 2, 10 (2020).
https://doi.org/10.1007/s42484-020-00021-x

[35] A. Cervera-Lierta, Quantum 2, 114 (2018).
https://doi.org/10.22331/q-2018-12-21-114

[36] K. Yeter-Aydeniz, R. C. Pooser, and G. Siopsis, npj Quantum Inf. 6, 63 (2020).
https://doi.org/10.1038/s41534-020-00290-1

[37] G. E. Volovik, JETP Lett. 70, 609 (1999).
https://doi.org/10.1134/1.568223

[38] N. Read, and D. Green, Phys. Rev. B 61, 10267 (2000).
https://doi.org/10.1103/PhysRevB.61.10267

[39] T. Fukui, Y. Hutsugai, and H. Suzuki, J. Phys. Soc. Jpn. 74, 1674 (2005).
https://doi.org/10.1143/JPSJ.74.1674

[40] P. J. J. O'malley, et al. Phys. Rev. X 6, 031007 (2016).
https://doi.org/10.1103/PhysRevX.6.031007

[41] A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow, and J. M. Gambetta, Nature 549, 242 (2017).
https://doi.org/10.1038/nature23879

[42] C. Kokail, C. Maier, R. van Bijnen, T. Brydges, M. K. Joshi, P. Jurcevic, C. A. Muschik, P. Silvi, R. Blatt, C. F. Roos, and P. Zoller, Nature 569, 355 (2019).
https://doi.org/10.1038/s41586-019-1177-4

[43] X. Yaun, S. Endo, Q. Zhao, Y. Li and S. C. Benjamin, Quantum 3, 191 (2019).
https://doi.org/10.22331/q-2019-10-07-191

[44] H. R. Grimsley, S. E. Economou, E. Barnes, and N. J. Mayhall Nat. Commun. 10, 3007 (2019).
https://doi.org/10.1038/s41467-019-10988-2

[45] Y. Hatsugai, and M. Kohmoto, J. Phys. Soc. Jpn 61, 2056 (1992).
https://doi.org/10.1143/JPSJ.61.2056

[46] K. Kudo, H. Watanabe, T. Kariyado, and Y. Hatsugai, Phys. Rev. Lett. 122, 146601 (2019).
https://doi.org/10.1103/PhysRevLett.122.146601

[47] P. W. Philips, L. Yeo, and E. W. Huang Nat. Phys. 16, 1175 (2020).
https://doi.org/10.1038/s41567-020-0988-4

[48] X.-L. Qi, Y. S. Wu and S. C. Zhang, Phys. Rev. B 74, 085308 (2006).
https://doi.org/10.1103/PhysRevB.74.085308

[49] H.-Q. Wu, Y.-Y. He, C. Fang, Z. Y. Meng and Z.-Y. Lu, Phys. Rev. Lett. 117, 066403 (2016).
https://doi.org/10.1103/PhysRevLett.117.066403

[50] C.-E. Bardyn, L. Wawer, A. Altland, M. Fleischhauer, and S. Diehl, Phys. Rev. X 8, 011035 (2018).
https://doi.org/10.1103/PhysRevX.8.011035

[51] D. Aharonov, V. Jones, and Z. Landau, Algorithmica 55, 395 (2009).
https://doi.org/10.1007/s00453-008-9168-0

[52] B. Murta, G. Catarina, J. Fernandez-Rossier Phys. Rev. A 101, 020302 (2020).
https://doi.org/10.1103/PhysRevA.101.020302

[53] G. Aleksandrowicz, et al. Qiskit: An open-source framework for quantum computing. (2019).
https://doi.org/10.5281/ZENODO.2562111

[54] E. Knill, Nature 434, 39 (2005).
https://doi.org/10.1038/nature03350

[55] A. Cross, D. P. Divincenzo, and B. M. Terhal, Quantum Info. Comput. 9, 541 (2009).
https://doi.org/10.48550/arXiv.0711.1556

[56] J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, J. Chem. Theory Comput. 15, 311 (2019).
https://doi.org/10.1021/acs.jctc.8b01004

[57] J. Chen, H.-P. Cheng and J. K. Freericks, J. Chem. Theory Comput. 17, 841 (2021).
https://doi.org/10.1021/acs.jctc.0c01052

[58] Y. Yao, F. Zhang, C.-Z. Wang, K.-M. Ho, and P. P. Orth Phys. Rev. Research 3, 013184 (2021).
https://doi.org/10.1103/PhysRevResearch.3.013184

[59] K. Mitarai and K. Fujii, Phys. Rev. Reseach 1, 013006 (2019).
https://doi.org/10.1103/PhysRevResearch.1.013006

[60] Z.-P. Cian, H. Dehghani, A. Elben, B. Vermersch, G. Zhu, M. Barkeshli, P. Zoller, and M. Hafezi, Phys. Rev. Lett. 126, 050501 (2021).
https://doi.org/10.1103/PhysRevLett.126.050501

[61] I. G. Ryabinkin, T.-C. Yen, S. N. Genin, and A. F. Izmaylov, J. Chem. Theory Comput. 14, 6317 (2018).
https://doi.org/10.1021/acs.jctc.8b00932

[62] M. Motta, C. Sun, A. T. Tan, M. J. O'Rourke, E. Ye, A. J. Minnich, F. G. Brandao, G. K.-L. Chan, Nat. Phys. 16, 205 (2020).
https://doi.org/10.1038/s41567-019-0704-4

[63] D. A. Fedorov, B. Peng, N. Govind, and Y. Alexeev, arXiv: 2103.08505 (2021).
https://doi.org/10.48550/arXiv.2103.08505

Cited by

[1] Zijian Liang, Yijia Xu, Joseph T. Iosue, and Yu-An Chen, "Extracting Topological Orders of Generalized Pauli Stabilizer Codes in Two Dimensions", PRX Quantum 5 3, 030328 (2024).

[2] Ze-Min Huang and Sebastian Diehl, "Interaction-Induced Topological Phase Transition at Finite Temperature", Physical Review Letters 134 5, 053002 (2025).

[3] Martin Mootz and Yong-Xin Yao, "Efficient Berry phase calculation via adaptive variational quantum computing approach", APL Quantum 3 1, 016111 (2026).

[4] Kevin Lively, Tim Bode, Jochen Szangolies, Jian-Xin Zhu, and Benedikt Fauseweh, "Noise robust detection of quantum phase transitions", Physical Review Research 6 4, 043254 (2024).

[5] Emiel Koridon, Joana Fraxanet, Alexandre Dauphin, Lucas Visscher, Thomas E. O'Brien, and Stefano Polla, "A hybrid quantum algorithm to detect conical intersections", Quantum 8, 1259 (2024).

[6] Marcel Niedermeier, Marc Nairn, Christian Flindt, and Jose L. Lado, "Quantum computing topological invariants of two-dimensional quantum matter", Physical Review Research 6 4, 043288 (2024).

[7] Jin Ming Koh, Tommy Tai, and Ching Hua Lee, "Realization of higher-order topological lattices on a quantum computer", Nature Communications 15 1, 5807 (2024).

[8] Huai-Chun Chang, Hsiu-Chuan Hsu, and Yu-Cheng Lin, "Probing entanglement dynamics and topological transitions on noisy intermediate-scale quantum computers", Physical Review Research 7 1, 013043 (2025).

[9] Amara Katabarwa, Katerina Gratsea, Athena Caesura, and Peter D. Johnson, "Early Fault-Tolerant Quantum Computing", PRX Quantum 5 2, 020101 (2024).

[10] Cleoner S. Pietralonga and Wendel S. Paz, "Probing shift-current responses in noncentrosymmetric materials using quantum algorithms", Materials Today Quantum 10, 100066 (2026).

[11] Efekan Kökcü, Daan Camps, Lindsay Bassman, J. K. Freericks, Wibe A. de Jong, Roel Van Beeumen, and Alexander F. Kemper, "Algebraic compression of quantum circuits for Hamiltonian evolution", Physical Review A 105 3, 032420 (2022).

[12] Takanori Sugimoto, "Quantum-circuit algorithms for many-body topological invariant and Majorana zero mode", arXiv:2304.13408, (2023).

[13] Huai-Chun Chang and Hsiu-Chuan Hsu, "Digital quantum simulation of dynamical topological invariants on near-term quantum computers", Quantum Information Processing 21 1, 41 (2022).

The above citations are from Crossref's cited-by service (last updated successfully 2026-08-09 13:08:01) and SAO/NASA ADS (last updated successfully 2026-08-09 13:08:05). The list may be incomplete as not all publishers provide suitable and complete citation data.

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.