Hybrid divide-and-conquer approach for tree search algorithms
1Laboratoire de Physique de l’Ecole Normale Supérieure, Inria, CNRS, ENS-PSL, Mines-Paristech, Sorbonne Université, PSL Research University, Paris, France
2LIACS, Leiden University, Leiden, The Netherlands
| Published: | 2023-03-23, volume 7, page 959 |
| Eprint: | arXiv:2007.07040v4 |
| Doi: | https://doi.org/10.22331/q-2023-03-23-959 |
| Citation: | Quantum 7, 959 (2023). |
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
One of the challenges of quantum computers in the near- and mid- term is the limited number of qubits we can use for computations. Finding methods that achieve useful quantum improvements under size limitations is thus a key question in the field. In this vein, it was recently shown that a hybrid classical-quantum method can help provide polynomial speed-ups to classical divide-and-conquer algorithms, even when only given access to a quantum computer much smaller than the problem itself. In this work, we study the hybrid divide-and-conquer method in the context of tree search algorithms, and extend it by including quantum backtracking, which allows better results than previous Grover-based methods. Further, we provide general criteria for polynomial speed-ups in the tree search context, and provide a number of examples where polynomial speed ups, using arbitrarily smaller quantum computers, can be obtained. We provide conditions for speedups for the well known algorithm of DPLL, and we prove threshold-free speed-ups for the PPSZ algorithm (the core of the fastest exact Boolean satisfiability solver) for well-behaved classes of formulas. We also provide a simple example where speed-ups can be obtained in an algorithm-independent fashion, under certain well-studied complexity-theoretical assumptions. Finally, we briefly discuss the fundamental limitations of hybrid methods in providing speed-ups for larger problems.
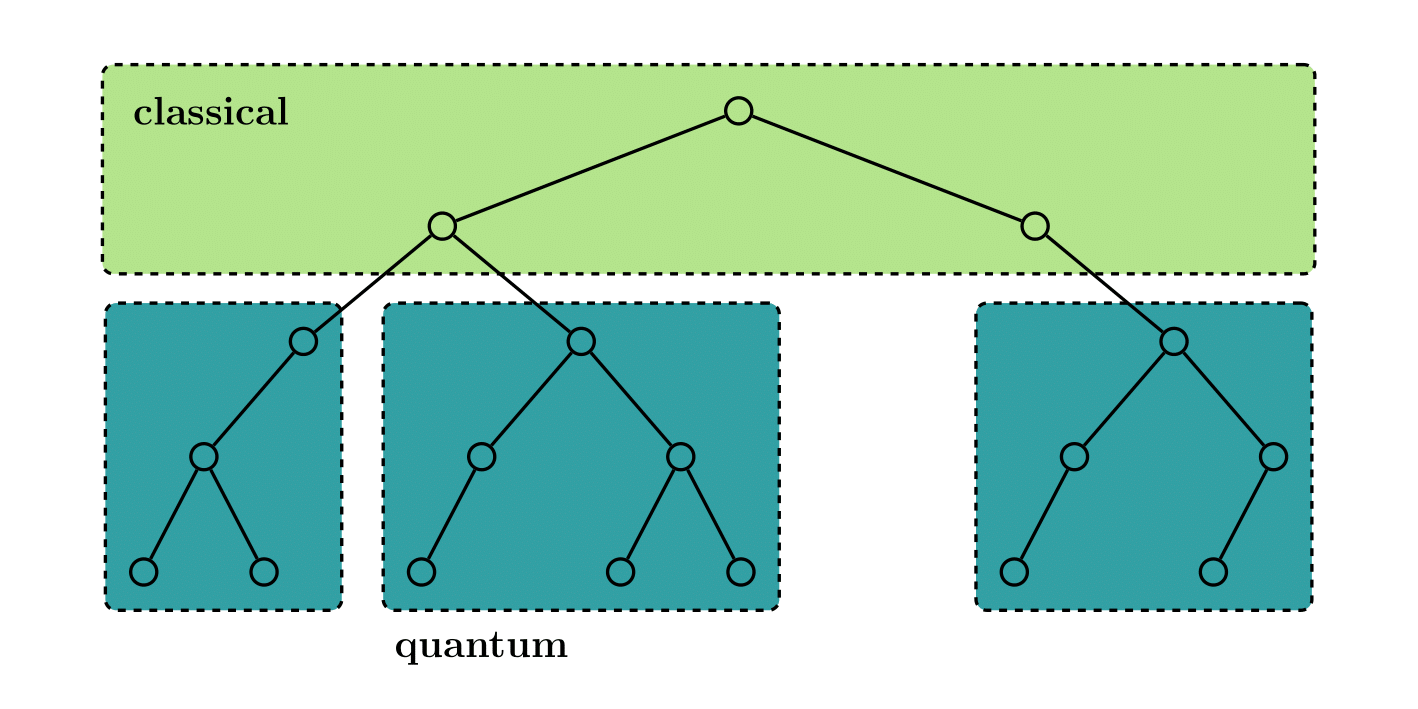
Popular summary
Tree search algorithms are particularly suited for this hybrid approach. When the search space is a complete binary tree it is straightforward to split the problem up into parts small enough for a given quantum computer and still be left with a (smaller) quantum speedup on the initial problem. However, in most classical tree search algorithms branches are pruned during the search and a sparser tree remains. In this setting, it becomes less obvious if a small polynomial speedup can still be obtained by a hybrid algorithm.
In this paper, we study this hybrid divide-and-conquer method in the context of tree search algorithms, such as the algorithms developed for Boolean satisfiability. Our main contribution is that we provide sufficient conditions for quantum speedups and apply them to two well-known Boolean satisfiability algorithms.
► BibTeX data
► References
[1] Vedran Dunjko, Yimin Ge, and J Ignacio Cirac. ``Computational speedups using small quantum devices''. Physical review letters 121, 250501 (2018).
https://doi.org/10.1103/PhysRevLett.121.250501
[2] Yimin Ge and Vedran Dunjko. ``A hybrid algorithm framework for small quantum computers with application to finding hamiltonian cycles''. Journal of Mathematical Physics 61, 012201 (2020).
https://doi.org/10.1063/1.5119235
[3] Ashley Montanaro. ``Quantum-Walk Speedup of Backtracking Algorithms''. Theory of Computing 14, 1–24 (2018).
https://doi.org/10.4086/toc.2018.v014a015
[4] Martin Davis, George Logemann, and Donald W Loveland. ``A machine program for theorem-proving''. New York University, Institute of Mathematical Sciences. (1961).
https://doi.org/10.1145/368273.368557
[5] Ramamohan Paturi, Pavel Pudlák, Michael E Saks, and Francis Zane. ``An improved exponential-time algorithm for k-SAT''. Journal of the ACM (JACM) 52, 337–364 (2005).
https://doi.org/10.1145/1066100.1066101
[6] Earl Campbell, Ankur Khurana, and Ashley Montanaro. ``Applying quantum algorithms to constraint satisfaction problems''. Quantum 3, 167 (2019).
https://doi.org/10.22331/q-2019-07-18-167
[7] Simon Martiel and Maxime Remaud. ``Practical implementation of a quantum backtracking algorithm''. In International Conference on Current Trends in Theory and Practice of Informatics. Pages 597–606. Springer (2020).
https://doi.org/10.1007/978-3-030-38919-2_49
[8] Thomas Dueholm Hansen, Haim Kaplan, Or Zamir, and Uri Zwick. ``Faster k-sat algorithms using biased-ppsz''. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing. Pages 578–589. STOC 2019New York, NY, USA (2019). ACM.
https://doi.org/10.1145/3313276.3316359
[9] Armin Biere, Marijn Heule, and Hans van Maaren. ``Handbook of satisfiability''. Volume 185. IOS press. (2009).
[10] Marc Mezard, Marc Mezard, and Andrea Montanari. ``Information, physics, and computation''. Oxford University Press. (2009).
https://doi.org/10.1063/1.3397047
[11] Martin Davis and Hilary Putnam. ``A Computing Procedure for Quantification Theory''. J. ACM 7, 201–215 (1960).
https://doi.org/10.1145/321033.321034
[12] Marijn JH Heule, Matti Juhani Järvisalo, Martin Suda, et al. ``Solver and benchmark descriptions''. In Proceedings of SAT competition 2018. Department of Computer Science, University of Helsinki (2018). url: http://hdl.handle.net/10138/237063.
http://hdl.handle.net/10138/237063
[13] Robert Nieuwenhuis, Albert Oliveras, and Cesare Tinelli. ``Abstract DPLL and abstract DPLL modulo theories''. In International Conference on Logic for Programming Artificial Intelligence and Reasoning. Pages 36–50. Springer (2005).
https://doi.org/10.1007/978-3-540-32275-7_3
[14] Jasmin Christian Blanchette, Sascha Böhme, and Lawrence C Paulson. ``Extending Sledgehammer with SMT solvers''. Journal of automated reasoning 51, 109–128 (2013).
https://doi.org/10.1007/s10817-013-9278-5
[15] Daniel Rolf. ``Derandomization of PPSZ for unique-k-SAT''. In International Conference on Theory and Applications of Satisfiability Testing. Pages 216–225. Springer (2005).
https://doi.org/10.1007/11499107_16
[16] Dominik Scheder and John P Steinberger. ``PPSZ for general k-SAT-making Hertli's analysis simpler and 3-SAT faster''. In 32nd Computational Complexity Conference (CCC 2017). Volume 79, pages 9:1–9:15. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2017).
https://doi.org/10.4230/LIPIcs.CCC.2017.9
[17] Daniel Rolf. ``Improved bound for the PPSZ/schoning-algorithm for 3-SAT''. Journal on Satisfiability, Boolean Modeling and Computation 1, 111–122 (2006).
https://doi.org/10.3233/SAT190005
[18] Timon Hertli. ``3-SAT faster and simpler—unique-SAT bounds for PPSZ hold in general''. SIAM Journal on Computing 43, 718–729 (2014).
https://doi.org/10.1137/120868177
[19] Timon Hertli. ``Breaking the PPSZ barrier for unique 3-SAT''. In Automata, Languages, and Programming: 41st International Colloquium, ICALP 2014, Copenhagen, Denmark, July 8-11, 2014, Proceedings, Part I 41. Pages 600–611. Springer (2014).
https://doi.org/10.1007/978-3-662-43948-7_50
[20] Dominik Scheder. ``PPSZ is better than you think''. In 2021 IEEE 62nd Annual Symposium on Foundations of Computer Science (FOCS). Pages 205–216. (2022).
https://doi.org/10.1109/FOCS52979.2021.00028
[21] Lov K Grover. ``A fast quantum mechanical algorithm for database search''. In Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. Pages 212–219. (1996).
https://doi.org/10.1145/237814.237866
[22] Andris Ambainis. ``Quantum search algorithms''. ACM SIGACT News 35, 22–35 (2004).
https://doi.org/10.1145/992287.992296
[23] Andris Ambainis and Martins Kokainis. ``Quantum algorithm for tree size estimation, with applications to backtracking and 2-player games''. In Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing. Pages 989–1002. (2017).
https://doi.org/10.1145/3055399.3055444
[24] Michael Jarret and Kianna Wan. ``Improved quantum backtracking algorithms using effective resistance estimates''. Physical Review A 97, 022337 (2018).
https://doi.org/10.1103/PhysRevA.97.022337
[25] Dominic J. Moylett, Noah Linden, and Ashley Montanaro. ``Quantum speedup of the traveling-salesman problem for bounded-degree graphs''. Phys. Rev. A 95, 032323 (2017).
https://doi.org/10.1103/PhysRevA.95.032323
[26] Neil D. Jones and William T. Laaser. ``Complete problems for deterministic polynomial time''. Theoretical Computer Science 3, 105 – 117 (1976).
https://doi.org/10.1016/0304-3975(76)90068-2
[27] Raymond Greenlaw, H James Hoover, Walter L Ruzzo, et al. ``Limits to parallel computation: P-completeness theory''. Oxford University Press on Demand. (1995).
[28] Thomas Lengauer and Robert E Tarjan. ``Asymptotically tight bounds on time-space trade-offs in a pebble game''. Journal of the ACM (JACM) 29, 1087–1130 (1982).
https://doi.org/10.1145/322344.322354
[29] Charles H Bennett. ``Time/space trade-offs for reversible computation''. SIAM Journal on Computing 18, 766–776 (1989).
https://doi.org/10.1137/0218053
[30] T. Altman and Y. Igarashi. ``Roughly sorting: Sequential and parallel approach''. J. Inf. Process. 12, 154–158 (1989). url: http://id.nii.ac.jp/1001/00059782/.
http://id.nii.ac.jp/1001/00059782/
[31] Hong-Yu Liang and Jing He. ``Satisfiability with index dependency''. Journal of Computer Science and Technology 27, 668–677 (2012).
https://doi.org/10.1007/978-3-642-17517-6_7
[32] Marcello Benedetti, John Realpe-Gómez, and Alejandro Perdomo-Ortiz. ``Quantum-assisted Helmholtz machines: A quantum–classical deep learning framework for industrial datasets in near-term devices''. Quantum Science and Technology 3, 034007 (2018).
https://doi.org/10.1088/2058-9565/aabd98
[33] Aram W. Harrow. ``Small quantum computers and large classical data sets'' (2020) arXiv:2004.00026.
arXiv:2004.00026
[34] Michael A Nielsen and Isaac Chuang. ``Quantum computation and quantum information''. American Association of Physics Teachers. (2002).
https://doi.org/10.1017/CBO9780511976667
[35] Robert B. Griffiths and Chi-Sheng Niu. ``Semiclassical fourier transform for quantum computation''. Phys. Rev. Lett. 76, 3228–3231 (1996).
https://doi.org/10.1103/PhysRevLett.76.3228
[36] Robert Raussendorf and Hans J. Briegel. ``A one-way quantum computer''. Phys. Rev. Lett. 86, 5188–5191 (2001).
https://doi.org/10.1103/PhysRevLett.86.5188
[37] Thomas E O'Brien, Brian Tarasinski, and Barbara M Terhal. ``Quantum phase estimation of multiple eigenvalues for small-scale (noisy) experiments''. New Journal of Physics 21, 023022 (2019).
https://doi.org/10.1088/1367-2630/aafb8e
[38] Akshay Ajagekar, Travis Humble, and Fengqi You. ``Quantum computing based hybrid solution strategies for large-scale discrete-continuous optimization problems''. Computers & Chemical Engineering 132, 106630 (2020).
https://doi.org/10.1016/j.compchemeng.2019.106630
[39] Tianyi Peng, Aram W Harrow, Maris Ozols, and Xiaodi Wu. ``Simulating large quantum circuits on a small quantum computer''. Physical review letters 125, 150504 (2020).
https://doi.org/10.1103/PhysRevLett.125.150504
[40] Sergey Bravyi, Graeme Smith, and John A. Smolin. ``Trading classical and quantum computational resources''. Physical Review X 6 (2016).
https://doi.org/10.1103/physrevx.6.021043
[41] Martijn Swenne. ``Solving SAT on noisy quantum computers''. https://theses.liacs.nl/1725 (2019). Bachelor thesis.
https://theses.liacs.nl/1725
[42] Theodore J Yoder, Guang Hao Low, and Isaac L Chuang. ``Fixed-point quantum search with an optimal number of queries''. Physical review letters 113 (2014).
https://doi.org/10.1103/PhysRevLett.113.210501
[43] Alessandro Cosentino, Robin Kothari, and Adam Paetznick. ``Dequantizing Read-once Quantum Formulas''. In 8th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2013). Volume 22 of Leibniz International Proceedings in Informatics (LIPIcs), pages 80–92. Dagstuhl, Germany (2013). Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik.
https://doi.org/10.4230/LIPIcs.TQC.2013.80
[44] David A Barrington. ``Bounded-width polynomial-size branching programs recognize exactly those languages in NC1''. Journal of Computer and System Sciences 38, 150–164 (1989).
https://doi.org/10.1016/0022-0000(89)90037-8
Cited by
[1] Casper Gyurik, Chris Cade, and Vedran Dunjko, "Towards quantum advantage via topological data analysis", arXiv:2005.02607, (2020).
[2] Kyle E. C. Booth, Bryan O'Gorman, Jeffrey Marshall, Stuart Hadfield, and Eleanor Rieffel, "Quantum-accelerated constraint programming", Quantum 5, 550 (2021).
[3] Casper Gyurik, Chris Cade, and Vedran Dunjko, "Towards quantum advantage via topological data analysis", Quantum 6, 855 (2022).
The above citations are from SAO/NASA ADS (last updated successfully 2024-05-14 02:49:01). The list may be incomplete as not all publishers provide suitable and complete citation data.
On Crossref's cited-by service no data on citing works was found (last attempt 2024-05-14 02:49:00).
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.