Finite Rate QLDPC-GKP Coding Scheme that Surpasses the CSS Hamming Bound

Nithin Raveendran; Narayanan Rengaswamy; Filip Rozpędek; Ankur Raina; Liang Jiang; Bane Vasić

doi:10.22331/q-2022-07-20-767

Finite Rate QLDPC-GKP Coding Scheme that Surpasses the CSS Hamming Bound

Nithin Raveendran¹, Narayanan Rengaswamy¹, Filip Rozpędek², Ankur Raina³, Liang Jiang², and Bane Vasić¹

¹Department of Electrical and Computer Engineering, University of Arizona, Tucson, Arizona 85721, USA
²Pritzker School of Molecular Engineering, The University of Chicago, Chicago, IL 60637, USA
³Department of Electrical Engineering and Computer Sciences, Indian Institute of Science Education and Research, Bhopal, Madhya Pradesh 462066, India

Published:	2022-07-20, volume 6, page 767
Eprint:	arXiv:2111.07029v2
Doi:	https://doi.org/10.22331/q-2022-07-20-767
Citation:	Quantum 6, 767 (2022).

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

Quantum error correction has recently been shown to benefit greatly from specific physical encodings of the code qubits. In particular, several researchers have considered the individual code qubits being encoded with the continuous variable GottesmanKitaev-Preskill (GKP) code, and then imposed an outer discrete-variable code such as the surface code on these GKP qubits. Under such a concatenation scheme, the analog information from the inner GKP error correction improves the noise threshold of the outer code. However, the surface code has vanishing rate and demands a lot of resources with growing distance. In this work, we concatenate the GKP code with generic quantum low-density parity-check (QLDPC) codes and demonstrate a natural way to exploit the GKP analog information in iterative decoding algorithms. We first show the noise thresholds for two lifted product QLDPC code families, and then show the improvements of noise thresholds when the iterative decoder – a hardware-friendly min-sum algorithm (MSA) – utilizes the GKP analog information. We also show that, when the GKP analog information is combined with a sequential update schedule for MSA, the scheme surpasses the well-known CSS Hamming bound for these code families. Furthermore, we observe that the GKP analog information helps the iterative decoder in escaping harmful trapping sets in the Tanner graph of the QLDPC code, thereby eliminating or significantly lowering the error floor of the logical error rate curves. Finally, we discuss new fundamental and practical questions that arise from this work on channel capacity under GKP analog information, and on improving decoder design and analysis.

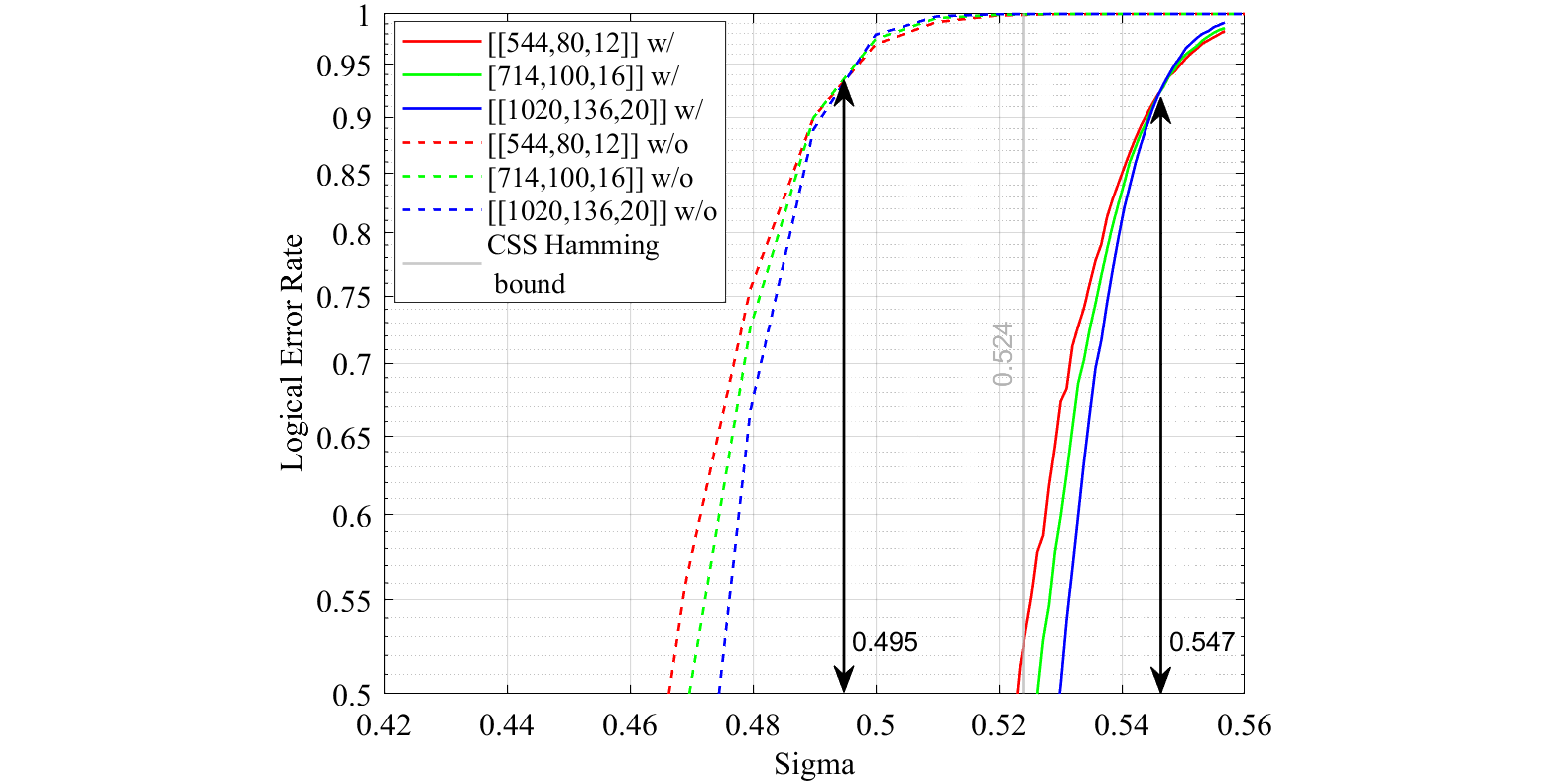
Featured image: GKP code concatenated with LP-QLDPC codes obtained from lifting regular quasi-cyclic LDPC codes of increasing code length and minimum distance. The dashed curves correspond to the sequential MSA decoder without using the analog information (from the inner GKP error correction), whereas the solid curves make use of the analog information for decoding the outer code. The transition of the curves with increasing σ signifies an error threshold, which is improved when decoding utilizes the analog information. Furthermore, the improved threshold for the code family surpasses the CSS Hamming bound highlighted as gray vertical lines at $\sigma$ = 0.524 demonstrating the advantage of GKP-QLDPC concatenation scheme.

Popular summary

We consider quantum error correction in a concatenated setting where the inner code is the continuous-variable square lattice Gottesman-Kitaev-Preskill (GKP) code and the outer code is chosen from a discrete-variable finite rate quantum low-density parity-check (QLDPC) code family. In this first work considering generic QLDPC codes as outer codes, we consider a simple noise model where the only source of noise is the Gaussian random displacement channel on each GKP data qubit, and all GKP ancillas used for syndrome measurements are infinitely squeezed (noiseless). The decoder for the outer code is the hardware-friendly min-sum algorithm (MSA), which is an approximation of the belief-propagation algorithm and is widely deployed in classical error correction applications. We show that the noise threshold for two lifted product QLDPC code families increase significantly when the MSA decoder for the outer QLDPC code appropriately leverages the GKP analog information from the inner GKP error correction. When the MSA decoder also uses a sequential node update schedule in addition to using the GKP analog information, our concatenated scheme surpasses the CSS Hamming bound (of C(p) = 1-2h(p), where p is related to the variance of the Gaussian random displacement) for these QLDPC code families. Usually BP based decoders for classical LDPC and QLDPC codes exhibit an error floor phenomenon where the logical error rate saturates at low channel error rates. But surprisingly, our simulations indicate that the GKP analog information seems to significantly lower the error floor or potentially eliminate it completely. These observations demonstrate the benefits of the finite rate QLDPC-GKP coding scheme. We also discuss several interesting questions that this work highlights, including the Hamming bound for degenerate codes, and the contribution of degeneracy of our considered QLDPC codes to surpassing the CSS Hamming bound.

► BibTeX data

@article{Raveendran2022finiterateqldpcgkp,
  doi = {10.22331/q-2022-07-20-767},
  url = {https://doi.org/10.22331/q-2022-07-20-767},
  title = {Finite {R}ate {QLDPC}-{GKP} {C}oding {S}cheme that {S}urpasses the {CSS} {H}amming {B}ound},
  author = {Raveendran, Nithin and Rengaswamy, Narayanan and Rozp{\k{e}}dek, Filip and Raina, Ankur and Jiang, Liang and Vasi{\'{c}}, Bane},
  journal = {{Quantum}},
  issn = {2521-327X},
  publisher = {{Verein zur F{\"{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}},
  volume = {6},
  pages = {767},
  month = jul,
  year = {2022}
}

► References

[1] D. J. C. MacKay, G. Mitchison, and P. L. McFadden, ``Sparse-graph codes for quantum error correction,'' IEEE Trans. Inf. Theory, vol. 50, no. 10, pp. 2315–2330, Oct. 2004. DOI: 10.1109/TIT.2004.834737.
https://doi.org/10.1109/TIT.2004.834737

[2] N. P. Breuckmann and J. N. Eberhardt, ``Quantum low-density parity-check codes,'' PRX Quantum, vol. 2, no. 4, p. 040101, Oct. 2021. DOI: 10.1103/PRXQuantum.2.040101.
https://doi.org/10.1103/PRXQuantum.2.040101

[3] D. Gottesman, ``Fault-tolerant quantum computation with constant overhead,'' Quantum Inf. and Computation, vol. 14, no. 15–16, pp. 1338–1372, Nov. 2014. DOI: 10.26421/QIC14.15-16-5.
https://doi.org/10.26421/QIC14.15-16-5

[4] M. B. Hastings, J. Haah, and R. O'Donnell, ``Fiber bundle codes: Breaking the $n^{1/2} \operatorname{polylog}(n)$ barrier for quantum LDPC codes,'' in Proc. of the 53rd Ann. ACM SIGACT Symp. on Theory of Computing, New York, NY, USA, 2021, pp. 1276–1288. DOI: 10.1145/3406325.3451005.
https://doi.org/10.1145/3406325.3451005

[5] S. Evra, T. Kaufman, and G. Zémor, ``Decodable quantum LDPC codes beyond the square root distance barrier using high dimensional expanders,'' SIAM J. on Computing, pp. FOCS20–276 FOCS20–316, 2020. DOI: 10.1137/20M1383689.
https://doi.org/10.1137/20M1383689

[6] P. Panteleev and G. Kalachev, ``Quantum LDPC codes with almost linear minimum distance,'' IEEE Trans. Inf. Theory, vol. 68, no. 1, pp. 213–229, Jan. 2022. DOI: 10.1109/TIT.2021.3119384.
https://doi.org/10.1109/TIT.2021.3119384

[7] N. P. Breuckmann and J. N. Eberhardt, ``Balanced product quantum codes,'' IEEE Trans. Inf. Theory, vol. 67, no. 10, pp. 6653–6674, Oct. 2021. DOI: 10.1109/TIT.2021.3097347.
https://doi.org/10.1109/TIT.2021.3097347

[8] P. Panteleev and G. Kalachev, ``Asymptotically good quantum and locally testable classical LDPC codes,'' arXiv preprint arXiv:2111.03654, 2021. DOI: 10.48550/ARXIV.2111.03654.
https://doi.org/10.48550/ARXIV.2111.03654
arXiv:2111.03654

[9] A. Leverrier and G. Zémor, ``Quantum Tanner codes,'' arXiv preprint arXiv:2202.13641, 2022. DOI: 10.48550/ARXIV.2202.13641.
https://doi.org/10.48550/ARXIV.2202.13641
arXiv:2202.13641

[10] O. Fawzi, A. Grospellier, and A. Leverrier, ``Efficient decoding of random errors for quantum expander codes,'' in Proc. 50th Ann. ACM SIGACT Symp. on Theory Computing, Los Angeles, CA, USA, 2018, pp. 521–534. DOI: 10.1145/3188745.3188886.
https://doi.org/10.1145/3188745.3188886

[11] W. Zeng and L. P. Pryadko, ``Higher-dimensional quantum hypergraph-product codes with finite rates,'' Phys. Rev. Lett., vol. 122, no. 23, p. 230501, Jun 2019. DOI: 10.1103/PhysRevLett.122.230501.
https://doi.org/10.1103/PhysRevLett.122.230501

[12] J.-P. Tillich and G. Zémor, ``Quantum LDPC codes with positive rate and minimum distance proportional to the square root of the blocklength,'' IEEE Trans. Inf. Theory, vol. 60, no. 2, pp. 1193–1202, 2014. DOI: 10.1109/TIT.2013.2292061.
https://doi.org/10.1109/TIT.2013.2292061

[13] D. Gottesman, A. Kitaev, and J. Preskill, ``Encoding a qubit in an oscillator,'' Phys. Rev. A, vol. 64, no. 1, p. 012310, Jun. 2001. DOI: 10.1103/PhysRevA.64.012310.
https://doi.org/10.1103/PhysRevA.64.012310

[14] K. Fukui, A. Tomita, and A. Okamoto, ``Analog quantum error correction with encoding a qubit into an oscillator,'' Phys. Rev. Lett., vol. 119, no. 18, p. 180507, Nov. 2017. DOI: 10.1103/PhysRevLett.119.180507.
https://doi.org/10.1103/PhysRevLett.119.180507

[15] K. Fukui, A. Tomita, A. Okamoto, and K. Fujii, ``High-threshold fault-tolerant quantum computation with analog quantum error correction,'' Phys. Rev. X, vol. 8, no. 2, p. 021054, May 2018. DOI: 10.1103/PhysRevX.8.021054.
https://doi.org/10.1103/PhysRevX.8.021054

[16] C. Vuillot, H. Asasi, Y. Wang, L. P. Pryadko, and B. M. Terhal, ``Quantum error correction with the toric Gottesman-Kitaev-Preskill code,'' Phys. Rev. A, vol. 99, no. 3, p. 032344, Mar. 2019. DOI: 10.1103/PhysRevA.99.032344.
https://doi.org/10.1103/PhysRevA.99.032344

[17] Y. Wang, ``Quantum error correction with the GKP code and concatenation with stabilizer codes,'' Master's thesis, RWTH-Aachen, 2019. DOI: 10.48550/ARXIV.1908.00147.
https://doi.org/10.48550/ARXIV.1908.00147

[18] B. M. Terhal, J. Conrad, and C. Vuillot, ``Towards scalable bosonic quantum error correction,'' Quantum Sci. Technol., vol. 5, no. 4, p. 043001, Jul. 2020. DOI: 10.1088/2058-9565/ab98a5.
https://doi.org/10.1088/2058-9565/ab98a5

[19] K. Noh and C. Chamberland, ``Fault-tolerant bosonic quantum error correction with the surface–Gottesman-Kitaev-Preskill code,'' Phys. Rev. A, vol. 101, no. 1, p. 012316, 2020. DOI: 10.1103/PhysRevA.101.012316.
https://doi.org/10.1103/PhysRevA.101.012316

[20] L. Hänggli, M. Heinze, and R. König, ``Enhanced noise resilience of the surface–Gottesman-Kitaev-Preskill code via designed bias,'' Phys. Rev. A, vol. 102, no. 5, p. 052408, 2020. DOI: 10.1103/PhysRevA.102.052408.
https://doi.org/10.1103/PhysRevA.102.052408

[21] K. Noh, C. Chamberland, and F. G. S. L. Brandão, ``Low-overhead fault-tolerant quantum error correction with the surface-GKP code,'' PRX Quantum, vol. 3, p. 010315, Jan 2022. DOI: 10.1103/PRXQuantum.3.010315.
https://doi.org/10.1103/PRXQuantum.3.010315

[22] K. Noh, ``Quantum computation and communication in bosonic systems,'' Ph.D. dissertation, Yale University, 2021. DOI: 10.48550/ARXIV.2103.09445.
https://doi.org/10.48550/ARXIV.2103.09445

[23] A. L. Grimsmo and S. Puri, ``Quantum error correction with the Gottesman-Kitaev-Preskill code,'' PRX Quantum, vol. 2, no. 2, p. 020101, 2021. DOI: 10.1103/PRXQuantum.2.020101.
https://doi.org/10.1103/PRXQuantum.2.020101

[24] F. Rozpędek, K. Noh, Q. Xu, S. Guha, and L. Jiang, ``Quantum repeaters based on concatenated bosonic and discrete-variable quantum codes,'' npj Quantum Inf., vol. 7, no. 1, pp. 1–12, 2021. DOI: 10.1038/s41534-021-00438-7.
https://doi.org/10.1038/s41534-021-00438-7

[25] A. R. Calderbank and P. W. Shor, ``Good quantum error-correcting codes exist,'' Phys. Rev. A, vol. 54, no. 2, pp. 1098–1105, Aug. 1996. DOI: 10.1103/physreva.54.1098.
https://doi.org/10.1103/physreva.54.1098

[26] A. M. Steane, ``Simple quantum error-correcting codes,'' Phys. Rev. A, vol. 54, no. 6, pp. 4741–4751, Dec. 1996. DOI: 10.1103/PhysRevA.54.4741.
https://doi.org/10.1103/PhysRevA.54.4741

[27] J. Chen, A. Dholakia, E. Eleftheriou, M. Fossorier, and X.-Y. Hu, ``Reduced-complexity decoding of LDPC codes,'' IEEE Trans. Commun., vol. 53, no. 8, pp. 1288–1299, Aug. 2005. DOI: 10.1109/TCOMM.2005.852852.
https://doi.org/10.1109/TCOMM.2005.852852

[28] D. E. Hocevar, ``A reduced complexity decoder architecture via layered decoding of LDPC codes,'' in Proc. IEEE Workshop on Signal Processing Systems, 2004, pp. 107–112. DOI: 10.1109/SIPS.2004.1363033.
https://doi.org/10.1109/SIPS.2004.1363033

[29] A. Steane, ``Multiple-particle interference and quantum error correction,'' Proc. Roy. Soc. Lon. A, vol. 452, no. 1954, pp. 2551–2577, 1996. DOI: 10.1098/rspa.1996.0136.
https://doi.org/10.1098/rspa.1996.0136

[30] E. Dennis, A. Kitaev, A. Landahl, and J. Preskill, ``Topological quantum memory,'' J. Math. Phys., vol. 43, no. 9, pp. 4452–4505, 2002. DOI: 10.1063/1.1499754.
https://doi.org/10.1063/1.1499754

[31] B. W. Walshe, B. Q. Baragiola, R. N. Alexander, and N. C. Menicucci, ``Continuous-variable gate teleportation and bosonic-code error correction,'' Phys. Rev. A, vol. 102, no. 6, p. 062411, 2020. DOI: 10.1103/PhysRevA.102.062411.
https://doi.org/10.1103/PhysRevA.102.062411

[32] K. Fukui, R. N. Alexander, and P. van Loock, ``All-optical long-distance quantum communication with Gottesman-Kitaev-Preskill qubits,'' Phys. Rev. Research, vol. 3, no. 3, p. 033118, 2021. DOI: 10.1103/PhysRevResearch.3.033118.
https://doi.org/10.1103/PhysRevResearch.3.033118

[33] K. Noh, V. V. Albert, and L. Jiang, ``Quantum capacity bounds of gaussian thermal loss channels and achievable rates with Gottesman-Kitaev-Preskill codes,'' IEEE Trans. Inf. Theory, vol. 65, no. 4, pp. 2563–2582, 2018. DOI: 10.1109/TIT.2018.2873764.
https://doi.org/10.1109/TIT.2018.2873764

[34] V. V. Albert, K. Noh, K. Duivenvoorden, D. J. Young, R. Brierley, P. Reinhold, C. Vuillot, L. Li, C. Shen, S. Girvin, B. M. Terhal, and L. Jiang, ``Performance and structure of single-mode bosonic codes,'' Phys. Rev. A, vol. 97, no. 3, p. 032346, Mar. 2018. DOI: 10.1103/PhysRevA.97.032346.
https://doi.org/10.1103/PhysRevA.97.032346

[35] M. G. Kim, N. Imoto, K. Cho, and M. S. Kim, ``Quantum noise in optical beam propagation in distributed amplifiers,'' Optics Communications, vol. 130, no. 4-6, pp. 377–384, 1996. DOI: 10.1016/0030-4018(96)00248-9.
https://doi.org/10.1016/0030-4018(96)00248-9

[36] K. K. Sabapathy, J. S. Ivan, and R. Simon, ``Robustness of non-gaussian entanglement against noisy amplifier and attenuator environments,'' Phys. Rev. Lett., vol. 107, no. 13, p. 130501, 2011. DOI: 10.1103/PhysRevLett.107.130501.
https://doi.org/10.1103/PhysRevLett.107.130501

[37] J. S. Ivan, K. K. Sabapathy, and R. Simon, ``Operator-sum representation for bosonic gaussian channels,'' Phys. Rev. A, vol. 84, no. 4, p. 042311, 2011. DOI: 10.1103/PhysRevA.84.042311.
https://doi.org/10.1103/PhysRevA.84.042311

[38] W.-L. Ma, S. Puri, R. J. Schoelkopf, M. H. Devoret, S. Girvin, and L. Jiang, ``Quantum control of bosonic modes with superconducting circuits,'' Science Bulletin, vol. 66, no. 17, pp. 1789–1805, 2021. DOI: 10.1016/j.scib.2021.05.024.
https://doi.org/10.1016/j.scib.2021.05.024

[39] P. Campagne-Ibarcq, A. Eickbusch, S. Touzard, E. Zalys-Geller, N. E. Frattini, V. V. Sivak, P. Reinhold, S. Puri, S. Shankar, R. J. Schoelkopf et al., ``Quantum error correction of a qubit encoded in grid states of an oscillator,'' Nature, vol. 584, no. 7821, pp. 368–372, 2020. DOI: 10.1038/s41586-020-2603-3.
https://doi.org/10.1038/s41586-020-2603-3

[40] C. Flühmann, T. L. Nguyen, M. Marinelli, V. Negnevitsky, K. Mehta, and J. Home, ``Encoding a qubit in a trapped-ion mechanical oscillator,'' Nature, vol. 566, no. 7745, pp. 513–517, 2019. DOI: 10.1038/s41586-019-0960-6.
https://doi.org/10.1038/s41586-019-0960-6

[41] B. de Neeve, T. L. Nguyen, T. Behrle, and J. Home, ``Error correction of a logical grid state qubit by dissipative pumping,'' Nature Phys., vol. 18, pp. 296–300, 2022. DOI: 10.1038/s41567-021-01487-7.
https://doi.org/10.1038/s41567-021-01487-7

[42] O. Fawzi, A. Grospellier, and A. Leverrier, ``Constant overhead quantum fault tolerance with quantum expander codes,'' Commun. ACM, vol. 64, no. 1, pp. 106–114, Dec. 2020. DOI: 10.1145/3434163.
https://doi.org/10.1145/3434163

[43] R. G. Gallager, Low Density Parity Check Codes. Cambridge, MA: M.I.T. Press, 1963. DOI: 10.7551/mitpress/4347.001.0001.
https://doi.org/10.7551/mitpress/4347.001.0001

[44] E. Sharon, S. Litsyn, and J. Goldberger, ``Efficient serial message-passing schedules for LDPC decoding,'' IEEE Trans. Inf. Theory, vol. 53, no. 11, pp. 4076–4091, 2007. DOI: 10.1109/TIT.2007.907507.
https://doi.org/10.1109/TIT.2007.907507

[45] D. Gottesman, ``Stabilizer codes and quantum error correction,'' Ph.D. dissertation, California Institute of Technology, 1997. DOI: 10.7907/rzr7-dt72.
https://doi.org/10.7907/rzr7-dt72

[46] J. Pearl, Probablisitic Reasoning in Intelligent Systems. San Francisco, CA: Kaufmann, 1988. DOI: 10.1016/C2009-0-27609-4.
https://doi.org/10.1016/C2009-0-27609-4

[47] F. R. Kschischang, B. J. Frey, and H. A. Loeliger, ``Factor graphs and the sum-product algorithm,'' IEEE Trans. Inf. Theory, vol. 47, no. 2, pp. 498–519, Feb. 2001. DOI: 10.1109/18.910572.
https://doi.org/10.1109/18.910572

[48] J. V. Coquillat, F. G. Herrero, N. Raveendran, and B. Vasić, ``Syndrome-based min-sum vs OSD-0 decoders: FPGA implementation and analysis for quantum LDPC codes,'' IEEE Access, vol. 9, pp. 138 734–138 743, Oct. 2021. DOI: 10.1109/ACCESS.2021.3118544.
https://doi.org/10.1109/ACCESS.2021.3118544

[49] A. A. Kovalev and L. P. Pryadko, ``Improved quantum hypergraph-product LDPC codes,'' in Proc. IEEE Intl. Symp. Inf. Theory, Jul. 2012, pp. 348–352. DOI: 10.1109/ISIT.2012.6284206.
https://doi.org/10.1109/ISIT.2012.6284206

[50] M. P. C. Fossorier, ``Quasicyclic low-density parity-check codes from circulant permutation matrices,'' IEEE Trans. Inf. Theory, vol. 50, no. 8, pp. 1788–1793, Aug. 2004. DOI: 10.1109/TIT.2004.831841.
https://doi.org/10.1109/TIT.2004.831841

[51] R. Tanner, D. Sridhara, A. Sridharan, T. Fuja, and J. Costello, D.J., ``LDPC block and convolutional codes based on circulant matrices,'' IEEE Trans. on Inf. Theory, vol. 50, no. 12, pp. 2966–2984, Dec. 2004. DOI: 10.1109/TIT.2004.838370.
https://doi.org/10.1109/TIT.2004.838370

[52] K.-Y. Kuo and C.-Y. Lai, ``Refined belief propagation decoding of sparse-graph quantum codes,'' IEEE J. Selected Areas in Inf. Theory, vol. 1, no. 2, pp. 487–498, 2020. DOI: 10.1109/jsait.2020.3011758.
https://doi.org/10.1109/jsait.2020.3011758

[53] N. Raveendran and B. Vasić, ``Trapping sets of quantum LDPC codes,'' Quantum, vol. 5, p. 562, Oct. 2021. DOI: 10.22331/q-2021-10-14-562.
https://doi.org/10.22331/q-2021-10-14-562

[54] P. Sarvepalli and A. Klappenecker, ``Degenerate quantum codes and the quantum hamming bound,'' Phys. Rev. A, vol. 81, no. 3, p. 032318, Mar. 2010. DOI: 10.1103/PhysRevA.81.032318.
https://doi.org/10.1103/PhysRevA.81.032318

[55] 4 T. J. Richardson, ``Error floors of LDPC codes,'' in Proc. 41st Ann. Allerton Conf. Commun., Contr. and Comp., Monticello, IL, USA, Sept. 2003, pp. 1426–1435. [Online]. Available: https://web.stanford.edu/class/ee388/papers/ErrorFloors.pdf 0pt.
https://web.stanford.edu/class/ee388/papers/ErrorFloors.pdf

[56] B. Vasić, D. Nguyen, and S. K. Chilappagari, ``Chapter 6 - Failures and error floors of iterative decoders,'' in Channel Coding: Theory, Algorithms, and Applications: Academic Press Library in Mobile and Wireless Commun. Oxford: Academic Press, 2014, pp. 299–341. DOI: 10.1016/B978-0-12-396499-1.00006-6.
https://doi.org/10.1016/B978-0-12-396499-1.00006-6

[57] J. Roffe, L. Z. Cohen, A. O. Quintivalle, D. Chandra, and E. T. Campbell, ``Bias-tailored quantum LDPC codes,'' arXiv preprint arXiv:2202.01702, 2022. DOI: 10.48550/ARXIV.2202.01702.
https://doi.org/10.48550/ARXIV.2202.01702
arXiv:2202.01702

[58] P. Fuentes, J. Etxezarreta, P. Crespo, and J. Garcia-Frias, ``Degeneracy and its impact on the decoding of sparse quantum codes,'' IEEE Access, vol. 9, pp. 89 093–89 119, Jun. 2021. DOI: 10.1109/ACCESS.2021.3089829.
https://doi.org/10.1109/ACCESS.2021.3089829

[59] C. A. Pattison, M. E. Beverland, M. P. da Silva, and N. Delfosse, ``Improved quantum error correction using soft information,'' arXiv preprint arXiv:2107.13589, 2021. DOI: 10.48550/ARXIV.2107.13589.
https://doi.org/10.48550/ARXIV.2107.13589
arXiv:2107.13589

[60] N. Raveendran, N. Rengaswamy, A. K. Pradhan, and B. Vasić, ``Soft syndrome decoding of quantum LDPC codes for joint correction of data and syndrome errors,'' arXiv preprint arXiv:2205.02341, 2022. DOI: 10.48550/ARXIV.2205.02341.
https://doi.org/10.48550/ARXIV.2205.02341
arXiv:2205.02341

[61] D. Declercq and M. Fossorier, ``Improved impulse method to evaluate the low weight profile of sparse binary linear codes,'' in Proc. IEEE Intl. Symp. Inf. Theory, 2008, pp. 1963–1967. DOI: 10.1109/ISIT.2008.4595332.
https://doi.org/10.1109/ISIT.2008.4595332

Cited by

[1] Yijia Xu, Yixu Wang, En-Jui Kuo, and Victor V. Albert, "Qubit-Oscillator Concatenated Codes: Decoding Formalism and Code Comparison", PRX Quantum 4 2, 020342 (2023).

[2] Nithin Raveendran, Narayanan Rengaswamy, Asit Kumar Pradhan, and Bane Vasic, 2022 IEEE International Conference on Quantum Computing and Engineering (QCE) 275 (2022) ISBN:978-1-6654-9113-6.

[3] Jing Wu, Anthony J. Brady, and Quntao Zhuang, "Optimal encoding of oscillators into more oscillators", Quantum 7, 1082 (2023).

[4] Sivaprasad Omanakuttan and T. J. Volkoff, "Spin-squeezed Gottesman-Kitaev-Preskill codes for quantum error correction in atomic ensembles", Physical Review A 108 2, 022428 (2023).

[5] Jing Wu, Anthony J. Brady, and Quntao Zhuang, CLEO 2023 FM4A.6 (2023) ISBN:978-1-957171-25-8.

[6] Nithin Raveendran, Narayanan Rengaswamy, Asit Kumar Pradhan, and Bane Vasić, "Soft Syndrome Decoding of Quantum LDPC Codes for Joint Correction of Data and Syndrome Errors", arXiv:2205.02341, (2022).

[7] Jonathan Conrad, Jens Eisert, and Jean-Pierre Seifert, "Good Gottesman-Kitaev-Preskill codes from the NTRU cryptosystem", arXiv:2303.02432, (2023).

[8] Narayanan Rengaswamy, Nithin Raveendran, Ankur Raina, and Bane Vasić, "Entanglement Purification with Quantum LDPC Codes and Iterative Decoding", arXiv:2210.14143, (2022).

The above citations are from Crossref's cited-by service (last updated successfully 2023-09-21 20:35:07) and SAO/NASA ADS (last updated successfully 2023-09-21 20:35:08). The list may be incomplete as not all publishers provide suitable and complete citation data.

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.