Spectrally multimode integrated SU(1,1) interferometer

Alessandro Ferreri; Matteo Santandrea; Michael Stefszky; Kai H. Luo; Harald Herrmann; Christine Silberhorn; Polina R. Sharapova

doi:10.22331/q-2021-05-27-461

Spectrally multimode integrated SU(1,1) interferometer

Alessandro Ferreri, Matteo Santandrea, Michael Stefszky, Kai H. Luo, Harald Herrmann, Christine Silberhorn, and Polina R. Sharapova

Department of Physics, Paderborn University, Warburger Strasse 100, D-33098 Paderborn, Germany

Published:	2021-05-27, volume 5, page 461
Eprint:	arXiv:2012.03751v2
Doi:	https://doi.org/10.22331/q-2021-05-27-461
Citation:	Quantum 5, 461 (2021).

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

Nonlinear SU(1,1) interferometers are fruitful and promising tools for spectral engineering and precise measurements with phase sensitivity below the classical bound. Such interferometers have been successfully realized in bulk and fiber-based configurations. However, rapidly developing integrated technologies provide higher efficiencies, smaller footprints, and pave the way to quantum-enhanced on-chip interferometry. In this work, we theoretically realised an integrated architecture of the multimode SU(1,1) interferometer which can be applied to various integrated platforms. The presented interferometer includes a polarization converter between two photon sources and utilizes a continuous-wave (CW) pump. Based on the potassium titanyl phosphate (KTP) platform, we show that this configuration results in almost perfect destructive interference at the output and supersensitivity regions below the classical limit. In addition, we discuss the fundamental difference between single-mode and highly multimode SU(1,1) interferometers in the properties of phase sensitivity and its limits. Finally, we explore how to improve the phase sensitivity by filtering the output radiation and using different seeding states in different modes with various detection strategies.

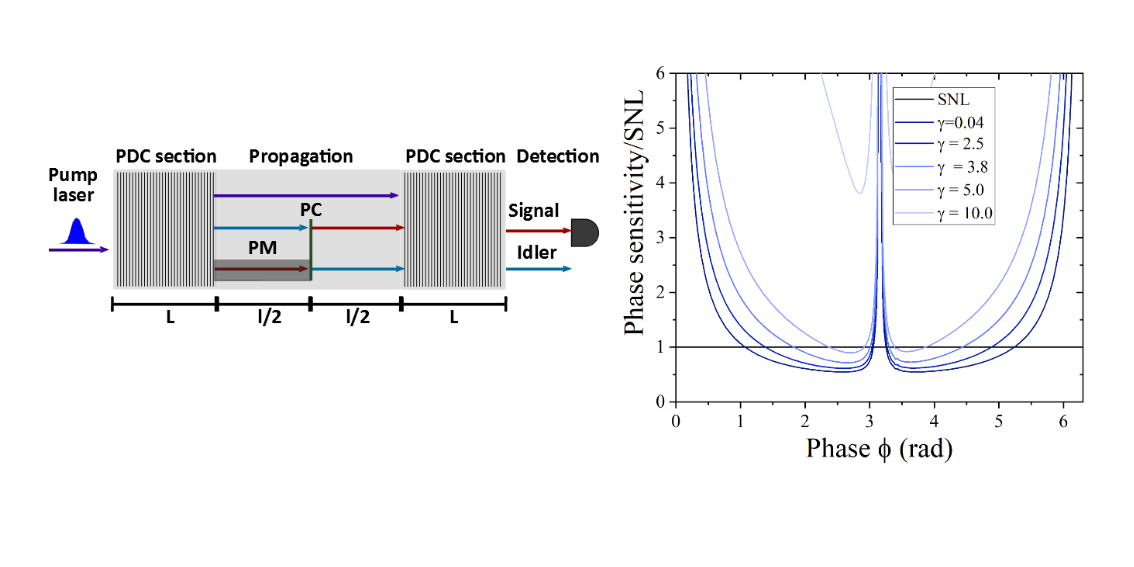
Featured image: On the left: schematic model of the integrated SU(1,1) interferometer. On the right: the phase sensitivity normalized to shot noise limit versus phase at different gains.

Popular summary

Interferometry has been a fundamental element in the history of Physics, and recently it got even a media impact during the first measurements of gravitational waves, beginning a revolution in Physics. The accuracy of interferometers is one of the main aims of metrology. It is well known that classical interferometers have a fundamental limitation of their precision, which, however, can be overcome using specific quantum light. Nonlinear interferometers, obtained by replacing beam splitters with nonlinear media, allow to beat the classical limit of accuracy even without preparing such exotic states of light. Despite the progressive implementation of new interferometer designs, current techniques did not include the spectral features of light in the phase sensitivity analysis, which, however, is very important due to multimodeness of photon sources. Finally, the tendency of miniaturization pushes the technology research to realize integrated devices, maintaining a high efficiency but reducing the footprint.

In this manuscript, we present an optimized design of an integrated nonlinear interferometer characterized by a wide range of spectral modes. The pondered design is based on real multimode photon sources and allows to compensate effects arising due to material dispersion, thereby maximizing the visibility of the interference pattern. The developed interferometer operates in a high sensitivity regime with an accuracy exceeding the classical bound, which has never been demonstrated in integrated platforms.

We believe that this work paves the way for a new class of high-performance integrated interferometers, which can have strong implications in future quantum technologies.

► BibTeX data

@article{Ferreri2021spectrallymultimode,
  doi = {10.22331/q-2021-05-27-461},
  url = {https://doi.org/10.22331/q-2021-05-27-461},
  title = {Spectrally multimode integrated {SU}(1,1) interferometer},
  author = {Ferreri, Alessandro and Santandrea, Matteo and Stefszky, Michael and Luo, Kai H. and Herrmann, Harald and Silberhorn, Christine and Sharapova, Polina R.},
  journal = {{Quantum}},
  issn = {2521-327X},
  publisher = {{Verein zur F{\"{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}},
  volume = {5},
  pages = {461},
  month = may,
  year = {2021}
}

► References

[1] M. V. Chekhovaand Z. Y. Ou ``Nonlinear interferometers in quantum optics'' Advances in Optics and Photonics 8, 104-155 (2016).
https://doi.org/10.1364/AOP.8.000104
http://aop.osa.org/abstract.cfm?URI=aop-8-1-104

[2] Carlton M. Caves ``Quantum-mechanical noise in an interferometer'' Physical Review D 23, 1693–1708 (1981).
https://doi.org/10.1103/PhysRevD.23.1693

[3] Carlton M. Caves ``Quantum limits on noise in linear amplifiers'' Physical Review D 26, 1817–1839 (1982).
https://doi.org/10.1103/PhysRevD.26.1817

[4] Rafal Demkowicz-Dobrzański, Marcin Jarzyna, and Jan Kołodyński, ``Chapter Four - Quantum Limits in Optical Interferometry'' Elsevier (2015).
https://doi.org/10.1016/bs.po.2015.02.003
http://www.sciencedirect.com/science/article/pii/S0079663815000049

[5] Sergei Slussarenko, Morgan M Weston, Helen M Chrzanowski, Lynden K Shalm, Varun B Verma, Sae Woo Nam, and Geoff J Pryde, ``Unconditional violation of the shot-noise limit in photonic quantum metrology'' Nature Photonics 11, 700 (2017).
https://doi.org/10.1038/s41566-017-0011-5

[6] Z. Y. Ou ``Fundamental quantum limit in precision phase measurement'' Physical Review A 55, 2598–2609 (1997).
https://doi.org/10.1103/PhysRevA.55.2598

[7] Jonathan P. Dowling ``Quantum optical metrology – the lowdown on high-N00N states'' Contemporary Physics 49, 125–143 (2008).
https://doi.org/10.1080/00107510802091298

[8] Bernard Yurke, Samuel L. McCall, and John R. Klauder, ``SU(2) and SU(1,1) interferometers'' Physical Review A 33, 4033–4054 (1986).
https://doi.org/10.1103/PhysRevA.33.4033

[9] U. Seyfarth, A. B. Klimov, H. de Guise, G. Leuchs, and L. L. Sanchez-Soto, ``Wigner function for SU(1,1)'' Quantum 4, 317 (2020).
https://doi.org/10.22331/q-2020-09-07-317

[10] Prasoon Gupta, Bonnie L. Schmittberger, Brian E. Anderson, Kevin M. Jones, and Paul D. Lett, ``Optimized phase sensing in a truncated SU(1,1) interferometer'' Optics Express 26, 391–401 (2018).
https://doi.org/10.1364/OE.26.000391
http://www.opticsexpress.org/abstract.cfm?URI=oe-26-1-391

[11] Carlton M. Caves ``Reframing SU(1,1) Interferometry'' Advanced Quantum Technologies 3, 1900138 (2020).
https://doi.org/10.1002/qute.201900138

[12] Mathieu Manceau, Farid Khalili, and Maria Chekhova, ``Improving the phase super-sensitivity of squeezing-assisted interferometers by squeeze factor unbalancing'' New Journal of Physics 19, 013014 (2017).
https://doi.org/10.1088/1367-2630/aa53d1

[13] Shengshuai Liu, Yanbo Lou, Jun Xin, and Jietai Jing, ``Quantum Enhancement of Phase Sensitivity for the Bright-Seeded SU(1,1) Interferometer with Direct Intensity Detection'' Physical Review Applied 10, 064046 (2018).
https://doi.org/10.1103/PhysRevApplied.10.064046

[14] Xiao Xiao, Hong-Bin Liang, Guo-Long Li, and Xiao-Guang Wang, ``Enhancement of Sensitivity by Initial Phase Matching in SU(1,1) Interferometers'' Communications in Theoretical Physics 71, 037 (2019).
https://doi.org/10.1088/0253-6102/71/1/37

[15] Mathieu Manceau, Gerd Leuchs, Farid Khalili, and Maria Chekhova, ``Detection Loss Tolerant Supersensitive Phase Measurement with an SU(1,1) Interferometer'' Physical Review Letters 119, 223604 (2017).
https://doi.org/10.1103/PhysRevLett.119.223604

[16] Enno Giese, Samuel Lemieux, Mathieu Manceau, Robert Fickler, and Robert W. Boyd, ``Phase sensitivity of gain-unbalanced nonlinear interferometers'' Physical Review A 96, 053863 (2017).
https://doi.org/10.1103/PhysRevA.96.053863

[17] Jefferson Flórez, Enno Giese, Davor Curic, Lambert Giner, Robert W Boyd, and Jeff S Lundeen, ``The phase sensitivity of a fully quantum three-mode nonlinear interferometer'' New Journal of Physics 20, 123022 (2018).
https://doi.org/10.1088/1367-2630/aaf3d2

[18] William N Plick, Jonathan P Dowling, and Girish S Agarwal, ``Coherent-light-boosted, sub-shot noise, quantum interferometry'' New Journal of Physics 12, 083014 (2010).
https://doi.org/10.1088/1367-2630/12/8/083014

[19] Brian E. Anderson, Bonnie L. Schmittberger, Prasoon Gupta, Kevin M. Jones, and Paul D. Lett, ``Optimal phase measurements with bright- and vacuum-seeded SU(1,1) interferometers'' Physical Review A 95, 063843 (2017).
https://doi.org/10.1103/PhysRevA.95.063843

[20] Dong Li, Chun-Hua Yuan, Z Y Ou, and Weiping Zhang, ``The phase sensitivity of an SU(1,1) interferometer with coherent and squeezed-vacuum light'' New Journal of Physics 16, 073020 (2014).
https://doi.org/10.1088/1367-2630/16/7/073020

[21] Sushovit Adhikari, Narayan Bhusal, Chenglong You, Hwang Lee, and Jonathan P. Dowling, ``Phase estimation in an SU(1,1) interferometer with displaced squeezed states'' OSA Continuum 1, 438–450 (2018).
https://doi.org/10.1364/OSAC.1.000438
http://www.osapublishing.org/osac/abstract.cfm?URI=osac-1-2-438

[22] Li-Li Guo, Ya-Fei Yu, and Zhi-Ming Zhang, ``Improving the phase sensitivity of an SU(1,1) interferometer with photon-added squeezed vacuum light'' Optics Express 26, 29099–29109 (2018).
https://doi.org/10.1364/OE.26.029099
http://www.opticsexpress.org/abstract.cfm?URI=oe-26-22-29099

[23] Xiaoping Ma, Chenglong You, Sushovit Adhikari, Elisha S. Matekole, Ryan T. Glasser, Hwang Lee, and Jonathan P. Dowling, ``Sub-shot-noise-limited phase estimation via SU(1,1) interferometer with thermal states'' Optics Express 26, 18492–18504 (2018).
https://doi.org/10.1364/OE.26.018492
http://www.opticsexpress.org/abstract.cfm?URI=oe-26-14-18492

[24] Jiamin Li, Yuhong Liu, Liang Cui, Nan Huo, Syed M. Assad, Xiaoying Li, and Z. Y. Ou, ``Joint measurement of multiple noncommuting parameters'' Physical Review A 97, 052127 (2018).
https://doi.org/10.1103/PhysRevA.97.052127

[25] Dong Li, Chun-Hua Yuan, Yao Yao, Wei Jiang, Mo Li, and Weiping Zhang, ``Effects of loss on the phase sensitivity with parity detection in an SU(1,1) interferometer'' Journal of the Optical Society of America B 35, 1080–1092 (2018).
https://doi.org/10.1364/JOSAB.35.001080
http://josab.osa.org/abstract.cfm?URI=josab-35-5-1080

[26] A. M. Marino, N. V. Corzo Trejo, and P. D. Lett, ``Effect of losses on the performance of an SU(1,1) interferometer'' Physical Review A 86, 023844 (2012).
https://doi.org/10.1103/PhysRevA.86.023844

[27] Jun Xin, Hailong Wang, and Jietai Jing, ``The effect of losses on the quantum-noise cancellation in the SU(1,1) interferometer'' Applied Physics Letters 109, 051107 (2016).
https://doi.org/10.1063/1.4960585

[28] Xiu-Ling Hu, Dong Li, L. Q. Chen, Keye Zhang, Weiping Zhang, and Chun-Hua Yuan, ``Phase estimation for an SU(1,1) interferometer in the presence of phase diffusion and photon losses'' Physical Review A 98, 023803 (2018).
https://doi.org/10.1103/PhysRevA.98.023803

[29] P. Sharapova, A. M. Pérez, O. V. Tikhonova, and M. V. Chekhova, ``Schmidt modes in the angular spectrum of bright squeezed vacuum'' Physical Review A 91, 043816 (2015).
https://doi.org/10.1103/PhysRevA.91.043816

[30] Gaetano Frascella, Roman V Zakharov, Olga V Tikhonova, and Maria V Chekhova, ``Experimental reconstruction of spatial Schmidt modes for a wide-field SU(1,1) interferometer'' Laser Physics 29, 124013 (2019).
https://doi.org/10.1088/1555-6611/ab4bdc

[31] Kirill A. Kuznetsov, Ekaterina I. Malkova, Roman V. Zakharov, Olga V. Tikhonova, and Galiya Kh. Kitaeva, ``Nonlinear interference in the strongly nondegenerate regime and Schmidt mode analysis'' Physical Review A 101, 053843 (2020).
https://doi.org/10.1103/PhysRevA.101.053843

[32] P. R. Sharapova, O. V. Tikhonova, S. Lemieux, R. W. Boyd, and M. V. Chekhova, ``Bright squeezed vacuum in a nonlinear interferometer: Frequency and temporal Schmidt-mode description'' Physical Review A 97, 053827 (2018).
https://doi.org/10.1103/PhysRevA.97.053827

[33] Samuel Lemieux, Mathieu Manceau, Polina R. Sharapova, Olga V. Tikhonova, Robert W. Boyd, Gerd Leuchs, and Maria V. Chekhova, ``Engineering the Frequency Spectrum of Bright Squeezed Vacuum via Group Velocity Dispersion in an SU(1,1) Interferometer'' Physical Review Letters 117, 183601 (2016).
https://doi.org/10.1103/PhysRevLett.117.183601

[34] Gil Triginer, Mihai D. Vidrighin, Nicolás Quesada, Andreas Eckstein, Merritt Moore, W. Steven Kolthammer, J. E. Sipe, and Ian A. Walmsley, ``Understanding High-Gain Twin-Beam Sources Using Cascaded Stimulated Emission'' Physical Review X 10, 031063 (2020).
https://doi.org/10.1103/PhysRevX.10.031063

[35] Anna V Paterovaand Leonid A Krivitsky ``Nonlinear interference in crystal superlattices'' Light: Science & Applications 9, 1–7 (2020).
https://doi.org/10.1038/s41377-020-0320-1

[36] G. Frascella, E. E. Mikhailov, N. Takanashi, R. V. Zakharov, O. V. Tikhonova, and M. V. Chekhova, ``Wide-field SU(1,1) interferometer'' Optica 6, 1233–1236 (2019).
https://doi.org/10.1364/OPTICA.6.001233
http://www.osapublishing.org/optica/abstract.cfm?URI=optica-6-9-1233

[37] Z. Y. Ouand Xiaoying Li ``Quantum SU(1,1) interferometers: Basic principles and applications'' APL Photonics 5, 080902 (2020).
https://doi.org/10.1063/5.0004873

[38] Jie Su, Liang Cui, Jiamin Li, Yuhong Liu, Xiaoying Li, and Z. Y. Ou, ``Versatile and precise quantum state engineering by using nonlinear interferometers'' Optics Express 27, 20479–20492 (2019).
https://doi.org/10.1364/OE.27.020479

[39] Joseph M. Lukens, Raphael C. Pooser, and Nicholas A. Peters, ``A broadband fiber-optic nonlinear interferometer'' Applied Physics Letters 113, 091103 (2018).
https://doi.org/10.1063/1.5048198

[40] Jeremy O'Brien, Brian Patton, Masahide Sasaki, and Jelena Vuc̆ković, ``Focus on integrated quantum optics'' New Journal of Physics 15, 035016 (2013).
https://doi.org/10.1088/1367-2630/15/3/035016

[41] S. Tanzilli, A. Martin, F. Kaiser, M.P. De Micheli, O. Alibart, and D.B. Ostrowsky, ``On the genesis and evolution of Integrated Quantum Optics'' Laser & Photonics Reviews 6, 115–143 (2012).
https://doi.org/10.1002/lpor.201100010

[42] Takafumi Ono, Gary F. Sinclair, Damien Bonneau, Mark G. Thompson, Jonathan C. F. Matthews, and John G. Rarity, ``Observation of nonlinear interference on a silicon photonic chip'' Optics Letters 44, 1277–1280 (2019).
https://doi.org/10.1364/OL.44.001277
http://ol.osa.org/abstract.cfm?URI=ol-44-5-1277

[43] Justin B. Spring, Benjamin J. Metcalf, Peter C. Humphreys, W. Steven Kolthammer, Xian-Min Jin, Marco Barbieri, Animesh Datta, Nicholas Thomas-Peter, Nathan K. Langford, Dmytro Kundys, James C. Gates, Brian J. Smith, Peter G. R. Smith, and Ian A. Walmsley, ``Boson Sampling on a Photonic Chip'' Science 339, 798–801 (2013).
https://doi.org/10.1126/science.1231692
https://science.sciencemag.org/content/339/6121/798

[44] Alberto Peruzzo, Mirko Lobino, Jonathan C. F. Matthews, Nobuyuki Matsuda, Alberto Politi, Konstantinos Poulios, Xiao-Qi Zhou, Yoav Lahini, Nur Ismail, Kerstin Wörhoff, Yaron Bromberg, Yaron Silberberg, Mark G. Thompson, and Jeremy L. OBrien, ``Quantum Walks of Correlated Photons'' Science 329, 1500–1503 (2010).
https://doi.org/10.1126/science.1193515
https://science.sciencemag.org/content/329/5998/1500

[45] P R Sharapova, K H Luo, H Herrmann, M Reichelt, T Meier, and C Silberhorn, ``Toolbox for the design of LiNbO3-based passive and active integrated quantum circuits'' New Journal of Physics 19, 123009 (2017).
https://doi.org/10.1088/1367-2630/aa9033

[46] DN Klyshko ``Ramsey interference in two-photon parametric scattering'' Journal of Experimental and Theoretical Physics 104, 2676–2684 (1993).
http://www.jetp.ac.ru/cgi-bin/e/index/e/77/2/p222?a=list

[47] DN Klyshko ``Parametric generation of two-photon light in anisotropic layered media'' Journal of Experimental and Theoretical Physics 105, 1574–1582 (1994).
http://www.jetp.ac.ru/cgi-bin/e/index/e/78/6/p848?a=list

[48] Matteo Santandrea, Michael Stefszky, Vahid Ansari, and Christine Silberhorn, ``Fabrication limits of waveguides in nonlinear crystals and their impact on quantum optics applications'' New Journal of Physics 21, 033038 (2019).
https://doi.org/10.1088/1367-2630/aaff13

[49] Sten Helmfrid, Gunnar Arvidsson, and Jonas Webjörn, ``Influence of various imperfections on the conversion efficiency of second-harmonic generation in quasi-phase-matching lithium niobate waveguides'' Journal of the Optical Society of America B 10, 222–229 (1993).
https://doi.org/10.1364/JOSAB.10.000222
http://josab.osa.org/abstract.cfm?URI=josab-10-2-222

[50] David S. Humand Martin M. Fejer ``Quasi-phasematching'' Comptes Rendus Physique 8, 180–198 (2007) Recent advances in crystal optic.
https://doi.org/10.1016/j.crhy.2006.10.022
http://www.sciencedirect.com/science/article/pii/S1631070506002349

Cited by

[1] N. Fabre and S. Felicetti, "Parameter estimation of time and frequency shifts with generalized Hong-Ou-Mandel interferometry", Physical Review A 104 2, 022208 (2021).

[2] Huanrong He, Shengshuai Liu, and Jietai Jing, "Enhancement of quadripartite quantum correlation via phase-sensitive cascaded four-wave mixing process", Physical Review A 107 2, 023702 (2023).

[3] Filippus S Roux, "Four-wave mixing in all degrees of freedom", Journal of Physics A: Mathematical and Theoretical 56 47, 475301 (2023).

[4] Alessandro Ferreri, Hannes Pfeifer, Frank K. Wilhelm, Sebastian Hofferberth, and David Edward Bruschi, "Interplay between optomechanics and the dynamical Casimir effect", Physical Review A 106 3, 033502 (2022).

[5] Matteo Santandrea, Kai-Hong Luo, Michael Stefszky, Jan Sperling, Harald Herrmann, Benjamin Brecht, and Christine Silberhorn, "Lossy SU(1,1) interferometers in the single-photon-pair regime", Quantum Science and Technology 8 2, 025020 (2023).

[6] Nicolas Fabre, Andrei B. Klimov, Gerd Leuchs, and Luis L. Sánchez-Soto, "Local sampling of the SU(1,1) Wigner function", AVS Quantum Science 5 1, 014404 (2023).

[7] Nicolas Fabre, Andrei B. Klimov, Gerd Leuchs, Luis L. Sanchez Soto, B. Kibler, G. Millot, and P. Segonds, "Local sampling of the SU(1,1) Wigner function", EPJ Web of Conferences 287, 06016 (2023).

[8] Filippus S. Roux, "Nonlinear interferometry in all spatiotemporal degrees of freedom", Physical Review A 105 4, 043701 (2022).

[9] Alessandro Ferreri and Polina Sharapova, "Two-Colour Spectrally Multimode Integrated SU(1,1) Interferometer", Symmetry 14 3, 552 (2022).

[10] Filippus S. Roux, "Stimulated parametric down-conversion for spatiotemporal metrology", Physical Review A 104 4, 043514 (2021).

[11] M. Genovese, "Experimental quantum enhanced optical interferometry", AVS Quantum Science 3 4, 044702 (2021).

[12] Pawan Kumar, Sina Saravi, Thomas Pertsch, Frank Setzpfandt, and Andrey A. Sukhorukov, "Nonlinear quantum spectroscopy with parity–time-symmetric integrated circuits", Photonics Research 10 7, 1763 (2022).

[13] Long Tian, Wenxiu Yao, Yimiao Wu, Qingwei Wang, Heng Shen, Yaohui Zheng, and Kunchi Peng, "Loss-tolerant and quantum-enhanced interferometer by reversed squeezing processes", Optics Letters 48 15, 3909 (2023).

[14] D. Scharwald, T. Meier, and P. R. Sharapova, "Phase sensitivity of spatially broadband high-gain SU(1,1) interferometers", Physical Review Research 5 4, 043158 (2023).

[15] Kai-Hong Luo, Matteo Santandrea, Michael Stefszky, Jan Sperling, Marcello Massaro, Alessandro Ferreri, Polina R. Sharapova, Harald Herrmann, and Christine Silberhorn, "Quantum optical coherence: From linear to nonlinear interferometers", Physical Review A 104 4, 043707 (2021).

[16] Kun Zhang, Yinghui Lv, Yu Guo, Jietai Jing, and Wu-Ming Liu, "Enhancing the precision of a phase measurement through phase-sensitive non-Gaussianity", Physical Review A 105 4, 042607 (2022).

[17] Dariya Salykina and Farid Khalili, "Sensitivity of Quantum-Enhanced Interferometers", Symmetry 15 3, 774 (2023).

The above citations are from Crossref's cited-by service (last updated successfully 2024-05-12 13:41:28) and SAO/NASA ADS (last updated successfully 2024-05-12 13:41:29). The list may be incomplete as not all publishers provide suitable and complete citation data.

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.