Combining hard and soft decoders for hypergraph product codes
1Inria, 2 Rue Simone IFF, CS 42112, 75589 Paris Cedex 12, France
2Université de Sherbrooke, 2500 Boulevard de l'Université, Sherbrooke, QC J1K 2R1, Canada
| Published: | 2021-04-15, volume 5, page 432 |
| Eprint: | arXiv:2004.11199v2 |
| Doi: | https://doi.org/10.22331/q-2021-04-15-432 |
| Citation: | Quantum 5, 432 (2021). |
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
Hypergraph product codes are a class of constant-rate quantum low-density parity-check (LDPC) codes equipped with a linear-time decoder called small-set-flip (SSF). This decoder displays sub-optimal performance in practice and requires very large error correcting codes to be effective. In this work, we present new hybrid decoders that combine the belief propagation (BP) algorithm with the SSF decoder. We present the results of numerical simulations when codes are subject to independent bit-flip and phase-flip errors. We provide evidence that the threshold of these codes is roughly 7.5% assuming an ideal syndrome extraction, and remains close to 3% in the presence of syndrome noise. This result subsumes and significantly improves upon an earlier work by Grospellier and Krishna (arXiv:1810.03681). The low-complexity high-performance of these heuristic decoders suggests that decoding should not be a substantial difficulty when moving from zero-rate surface codes to constant-rate LDPC codes and gives a further hint that such codes are well-worth investigating in the context of building large universal quantum computers.
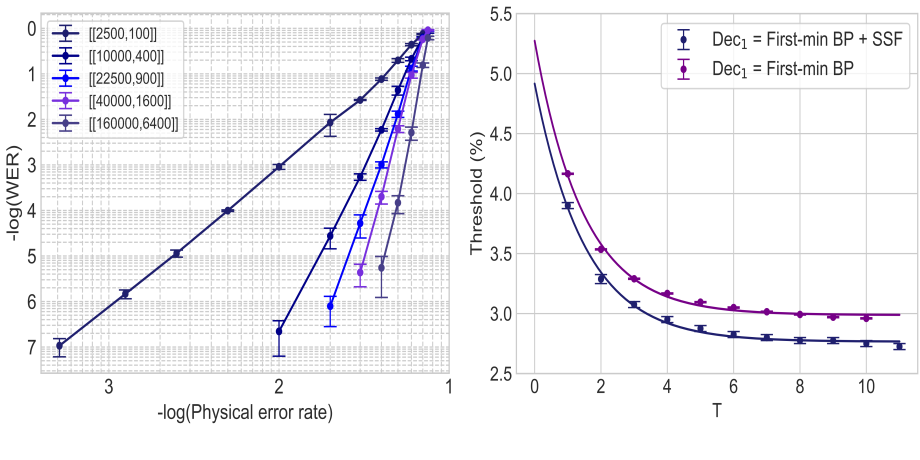
Featured image: A plot of the performance of a certain class of hypergraph product codes obtained from (3,4)-biregular bipartite graphs. These figures are evidence for the threshold and sustainable threshold respectively in instances where the syndrome extraction is ideal (left) and noisy (right).
Popular summary
While out of experimental reach currently, quantum low-density parity-check (LDPC) codes could be the answer in the long term. In theory, they promise a smaller resource cost compared to current techniques. However more research is needed before we can be certain whether this architecture is worth the experimental effort to explore. We take steps towards bridging this gap between theory and practice. To be specific, previous theoretical works only promise that quantum LDPC codes perform well for large quantum circuits. Part of the trouble stemmed from decoding algorithms, i.e. techniques to troubleshoot and correct errors. These algorithms seemed to require far too many qubits before becoming practical.
In this work, we pick a particular class of quantum LDPC codes called hypergraph product codes. We present new decoding algorithms, constructed as hybrids of classical and quantum decoding algorithms. We study different scenarios of increasing complexity, first assuming that the readout (syndrome extraction) can be done perfectly, and then working with models that assume that the readout itself is error prone. Our results show significant improvement over previous work and are supported by different metrics such as the (pseudo-)threshold and the weight of the parity checks. This provides evidence that such codes are well-worth investigating in the context of building large universal quantum computers.
► BibTeX data
► References
[1] Dorit Aharonov and Michael Ben-Or. Fault-tolerant quantum computation with constant error. In Proceedings of the twenty-ninth annual ACM symposium on Theory of computing, pages 176–188. ACM, 1997. 10.1137/S0097539799359385. URL https://doi.org/10.1137/S0097539799359385.
https://doi.org/10.1137/S0097539799359385
[2] Héctor Bombin, Ruben S Andrist, Masayuki Ohzeki, Helmut G Katzgraber, and Miguel A Martin-Delgado. Strong resilience of topological codes to depolarization. Physical Review X, 2 (2): 021004, 2012. 10.1103/PhysRevX.2.021004. URL https://link.aps.org/doi/10.1103/PhysRevX.2.021004.
https://doi.org/10.1103/PhysRevX.2.021004
[3] Sergey Bravyi, David Poulin, and Barbara Terhal. Tradeoffs for reliable quantum information storage in 2D systems. Physical Review Letters, 104 (5): 050503, 2010. 10.1103/PhysRevLett.104.050503. URL https://link.aps.org/doi/10.1103/PhysRevLett.104.050503.
https://doi.org/10.1103/PhysRevLett.104.050503
[4] Nikolas P Breuckmann and Vivien Londe. Single-Shot Decoding of Linear Rate LDPC Quantum Codes with High Performance. arXiv preprint arXiv:2001.03568, 2020.
arXiv:2001.03568
[5] Nikolas P Breuckmann and Barbara M Terhal. Constructions and noise threshold of hyperbolic surface codes. IEEE transactions on Information Theory, 62 (6): 3731–3744, 2016. 10.1109/TIT.2016.2555700.
https://doi.org/10.1109/TIT.2016.2555700
[6] Nikolas P Breuckmann, Christophe Vuillot, Earl Campbell, Anirudh Krishna, and Barbara M Terhal. Hyperbolic and semi-hyperbolic surface codes for quantum storage. Quantum Science and Technology, 2 (3): 035007, 2017. 10.1088/2058-9565/aa7d3b.
https://doi.org/10.1088/2058-9565/aa7d3b
[7] Benjamin J Brown, Naomi H Nickerson, and Dan E Browne. Fault-tolerant error correction with the gauge color code. Nature communications, 7 (1): 1–8, 2016. 10.1038/ncomms12302.
https://doi.org/10.1038/ncomms12302
[8] A Robert Calderbank and Peter W Shor. Good quantum error-correcting codes exist. Physical Review A, 54 (2): 1098, 1996. 10.1103/PhysRevA.54.1098.
https://doi.org/10.1103/PhysRevA.54.1098
[9] Christopher T Chubb and Steven T Flammia. Statistical mechanical models for quantum codes with correlated noise. arXiv preprint arXiv:1809.10704, 2018.
arXiv:1809.10704
[10] Jonathan Conrad, Christopher Chamberland, Nikolas P Breuckmann, and Barbara M Terhal. The small stellated dodecahedron code and friends. Phil. Trans. R. Soc. A, 376 (2123): 20170323, 2018. 10.1098/rsta.2017.0323.
https://doi.org/10.1098/rsta.2017.0323
[11] Nicolas Delfosse. Tradeoffs for reliable quantum information storage in surface codes and color codes. In Information Theory Proceedings (ISIT), 2013 IEEE International Symposium on, pages 917–921. IEEE, 2013. 10.1109/ISIT.2013.6620360.
https://doi.org/10.1109/ISIT.2013.6620360
[12] Eric Dennis, Alexei Kitaev, Andrew Landahl, and John Preskill. Topological quantum memory. Journal of Mathematical Physics, 43 (9): 4452–4505, 2002. 10.1063/1.1499754.
https://doi.org/10.1063/1.1499754
[13] Ilya Dumer, Alexey A Kovalev, and Leonid P Pryadko. Thresholds for correcting errors, erasures, and faulty syndrome measurements in degenerate quantum codes. Physical review letters, 115 (5): 050502, 2015. 10.1103/PhysRevLett.115.050502.
https://doi.org/10.1103/PhysRevLett.115.050502
[14] Omar Fawzi, Antoine Grospellier, and Anthony Leverrier. Constant overhead quantum fault-tolerance with quantum expander codes. In 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS), pages 743–754. IEEE, 2018a. 10.1109/FOCS.2018.00076.
https://doi.org/10.1109/FOCS.2018.00076
[15] Omar Fawzi, Antoine Grospellier, and Anthony Leverrier. Efficient decoding of random errors for quantum expander codes. In Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, pages 521–534. ACM, 2018b. 10.1145/3188745.3188886.
https://doi.org/10.1145/3188745.3188886
[16] Marc PC Fossorier and Shu Lin. Soft-decision decoding of linear block codes based on ordered statistics. IEEE Transactions on Information Theory, 41 (5): 1379–1396, 1995. 10.1109/18.412683.
https://doi.org/10.1109/18.412683
[17] Michael H Freedman, David A Meyer, and Feng Luo. Z2-systolic freedom and quantum codes. Mathematics of quantum computation, Chapman & Hall/CRC, pages 287–320, 2002.
[18] Daniel Gottesman. Stabilizer codes and quantum error correction. arXiv preprint quant-ph/9705052, 1997.
arXiv:quant-ph/9705052
[19] Daniel Gottesman. Fault-tolerant quantum computation with constant overhead. Quantum Information & Computation, 14 (15-16): 1338–1372, 2014. 10.5555/2685179.2685184.
https://doi.org/10.5555/2685179.2685184
[20] Antoine Grospellier and Anirudh Krishna. Numerical study of hypergraph product codes. arXiv preprint arXiv:1810.03681, 2018.
arXiv:1810.03681
[21] Larry Guth and Alexander Lubotzky. Quantum error correcting codes and 4-dimensional arithmetic hyperbolic manifolds. Journal of Mathematical Physics, 55 (8): 082202, 2014. 10.1063/1.4891487.
https://doi.org/10.1063/1.4891487
[22] A Yu Kitaev. Quantum computations: algorithms and error correction. Russian Mathematical Surveys, 52 (6): 1191–1249, 1997. 10.4213/rm892.
https://doi.org/10.4213/rm892
[23] Emanuel Knill, Raymond Laflamme, and Wojciech H Zurek. Resilient quantum computation: error models and thresholds. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, volume 454, pages 365–384. The Royal Society, 1998. 10.1126/science.279.5349.342.
https://doi.org/10.1126/science.279.5349.342
[24] Alexey A Kovalev and Leonid P Pryadko. Improved quantum hypergraph-product LDPC codes. In Information Theory Proceedings (ISIT), 2012 IEEE International Symposium on, pages 348–352. IEEE, 2012. 10.1109/ISIT.2012.6284206.
https://doi.org/10.1109/ISIT.2012.6284206
[25] Alexey A Kovalev and Leonid P Pryadko. Fault tolerance of quantum low-density parity check codes with sublinear distance scaling. Physical Review A, 87 (2): 020304, 2013. 10.1103/PhysRevA.87.020304.
https://doi.org/10.1103/PhysRevA.87.020304
[26] Alexey A Kovalev, Sanjay Prabhakar, Ilya Dumer, and Leonid P Pryadko. Numerical and analytical bounds on threshold error rates for hypergraph-product codes. Physical Review A, 97 (6): 062320, 2018. 10.1103/PhysRevA.97.062320.
https://doi.org/10.1103/PhysRevA.97.062320
[27] Anirudh Krishna and David Poulin. Topological wormholes: Nonlocal defects on the toric code. Phys. Rev. Research, 2: 023116, May 2020. 10.1103/PhysRevResearch.2.023116. URL https://link.aps.org/doi/10.1103/PhysRevResearch.2.023116.
https://doi.org/10.1103/PhysRevResearch.2.023116
[28] Anirudh Krishna and David Poulin. Fault-tolerant gates on hypergraph product codes. Phys. Rev. X, 11: 011023, Feb 2021. 10.1103/PhysRevX.11.011023. URL https://link.aps.org/doi/10.1103/PhysRevX.11.011023.
https://doi.org/10.1103/PhysRevX.11.011023
[29] Anthony Leverrier, Jean-Pierre Tillich, and Gilles Zémor. Quantum expander codes. In Foundations of Computer Science (FOCS), 2015 IEEE 56th Annual Symposium on, pages 810–824. IEEE, 2015. 10.1109/FOCS.2015.55.
https://doi.org/10.1109/FOCS.2015.55
[30] Muyuan Li and Theodore J. Yoder. A numerical study of bravyi-bacon-shor and subsystem hypergraph product codes. pages 109–119, 2020. 10.1109/QCE49297.2020.00024.
https://doi.org/10.1109/QCE49297.2020.00024
[31] Vivien Londe and Anthony Leverrier. Golden codes: quantum LDPC codes built from regular tessellations of hyperbolic 4-manifolds. Quantum Information & Computation, 19 (5-6): 361–391, 2019. 10.26421/QIC19.5-6.
https://doi.org/10.26421/QIC19.5-6
[32] Brendan D McKay and Xiaoji Wang. Asymptotic enumeration of 0–1 matrices with equal row sums and equal column sums. Linear algebra and its applications, 373: 273–287, 2003. 10.1016/S0024-3795(03)00506-8.
https://doi.org/10.1016/S0024-3795(03)00506-8
[33] Pavel Panteleev and Gleb Kalachev. Degenerate quantum ldpc codes with good finite length performance. arXiv preprint arXiv:1904.02703, 2019.
arXiv:1904.02703
[34] David Poulin and Yeojin Chung. On the iterative decoding of sparse quantum codes. Quantum Information & Computation, 8 (10): 987–1000, 2008. 10.5555/2016985.2016993.
https://doi.org/10.5555/2016985.2016993
[35] Tom Richardson and Ruediger Urbanke. Modern coding theory. Cambridge university press, 2008.
[36] Michael Sipser and Daniel A Spielman. Expander codes. In Foundations of Computer Science, 1994 Proceedings., 35th Annual Symposium on, pages 566–576. IEEE, 1994. 10.1109/18.556667.
https://doi.org/10.1109/18.556667
[37] Andrew Steane. Multiple-particle interference and quantum error correction. Proceedings of the Royal Society A, 452 (1954): 2551–2577, 1996. 10.1098/rspa.1996.0136.
https://doi.org/10.1098/rspa.1996.0136
[38] Jean-Pierre Tillich and Gilles Zémor. Quantum LDPC codes with positive rate and minimum distance proportional to the square root of the blocklength. IEEE Transactions on Information Theory, 60 (2): 1193–1202, 2014. 10.1109/TIT.2013.2292061.
https://doi.org/10.1109/TIT.2013.2292061
[39] Chenyang Wang, Jim Harrington, and John Preskill. Confinement-higgs transition in a disordered gauge theory and the accuracy threshold for quantum memory. Annals of Physics, 303 (1): 31–58, 2003. 10.1016/S0003-4916(02)00019-2.
https://doi.org/10.1016/S0003-4916(02)00019-2
[40] Weilei Zeng and Leonid P Pryadko. Higher-dimensional quantum hypergraph-product codes with finite rates. Physical Review Letters, 122 (23): 230501, 2019. 10.1103/PhysRevLett.122.230501.
https://doi.org/10.1103/PhysRevLett.122.230501
[41] Guanyu Zhu, Ali Lavasani, and Maissam Barkeshli. Instantaneous braids and dehn twists in topologically ordered states. Phys. Rev. B, 102: 075105, Aug 2020. 10.1103/PhysRevB.102.075105.
https://doi.org/10.1103/PhysRevB.102.075105
Cited by
[1] Kao-Yueh Kuo and Ching-Yi Lai, "Exploiting degeneracy in belief propagation decoding of quantum codes", npj Quantum Information 8 1, 111 (2022).
[2] Bochen Tan, Dolev Bluvstein, Mikhail D. Lukin, and Jason Cong, Proceedings of the 41st IEEE/ACM International Conference on Computer-Aided Design 1 (2022) ISBN:9781450392174.
[3] Aleksander Kubica and Michael Vasmer, "Single-shot quantum error correction with the three-dimensional subsystem toric code", Nature Communications 13 1, 6272 (2022).
[4] Kao-Yueh Kuo, I-Chun Chern, and Ching-Yi Lai, 2021 IEEE International Symposium on Information Theory (ISIT) 1552 (2021) ISBN:978-1-5386-8209-8.
[5] Daniel Bochen Tan, Dolev Bluvstein, Mikhail D. Lukin, and Jason Cong, "Compiling Quantum Circuits for Dynamically Field-Programmable Neutral Atoms Array Processors", Quantum 8, 1281 (2024).
[6] Qian Xu, J. Pablo Bonilla Ataides, Christopher A. Pattison, Nithin Raveendran, Dolev Bluvstein, Jonathan Wurtz, Bane Vasić, Mikhail D. Lukin, Liang Jiang, and Hengyun Zhou, "Constant-overhead fault-tolerant quantum computation with reconfigurable atom arrays", Nature Physics (2024).
[7] Lawrence Z. Cohen, Isaac H. Kim, Stephen D. Bartlett, and Benjamin J. Brown, "Low-overhead fault-tolerant quantum computing using long-range connectivity", Science Advances 8 20, eabn1717 (2022).
[8] Joschka Roffe, Lawrence Z. Cohen, Armanda O. Quintavalle, Daryus Chandra, and Earl T. Campbell, "Bias-tailored quantum LDPC codes", Quantum 7, 1005 (2023).
[9] T. R. Scruby and K. Nemoto, "Local Probabilistic Decoding of a Quantum Code", Quantum 7, 1093 (2023).
[10] Nikolas P. Breuckmann and Jens Niklas Eberhardt, "Quantum Low-Density Parity-Check Codes", PRX Quantum 2 4, 040101 (2021).
[11] Ning Bao, ChunJun Cao, and Guanyu Zhu, "Deconfinement and error thresholds in holography", Physical Review D 106 4, 046009 (2022).
[12] Nithin Raveendran, Emmanuel Boutillon, and Bane Vasić, 2023 12th International Symposium on Topics in Coding (ISTC) 1 (2023) ISBN:979-8-3503-2611-6.
[13] Javier Valls, Francisco Garcia-Herrero, Nithin Raveendran, and Bane Vasic, "Syndrome-Based Min-Sum vs OSD-0 Decoders: FPGA Implementation and Analysis for Quantum LDPC Codes", IEEE Access 9, 138734 (2021).
[14] Anthony Leverrier and Gilles Zémor, "Decoding Quantum Tanner Codes", IEEE Transactions on Information Theory 69 8, 5100 (2023).
[15] Wenting Zhou, Jie Liu, Bao Feng, Xiao Ye, Tianbing Zhang, Yuxiang Bian, and Wenjie Liu, Lecture Notes in Computer Science 13340, 271 (2022) ISBN:978-3-031-06790-7.
[16] Maxime Tremblay, Guillaume Duclos-Cianci, and Stefanos Kourtis, "Finite-rate sparse quantum codes aplenty", Quantum 7, 985 (2023).
[17] Ali Mohammed Kadhim, Wisam Subhi Al-dayyeni, and Majid S. Naghmash, Lecture Notes in Networks and Systems 584, 419 (2023) ISBN:978-3-031-25273-0.
[18] Josias Old and Manuel Rispler, "Generalized Belief Propagation Algorithms for Decoding of Surface Codes", Quantum 7, 1037 (2023).
[19] Maxime A. Tremblay, Nicolas Delfosse, and Michael E. Beverland, "Constant-Overhead Quantum Error Correction with Thin Planar Connectivity", Physical Review Letters 129 5, 050504 (2022).
[20] Zhengzhong Yi, Zhipeng Liang, and Xuan Wang, "Channel polarization of two-dimensional-input quantum symmetric channels", Quantum Information Processing 22 5, 209 (2023).
[21] Tzu-Hsuan Huang, Ting-An Hu, and Yeong-Luh Ueng, "Branch-Assisted Sign-Flipping Belief Propagation Decoding for Topological Quantum Codes Based on Hypergraph Product Structure", IEEE Transactions on Quantum Engineering 4, 1 (2023).
[22] Joschka Roffe, David R. White, Simon Burton, and Earl Campbell, "Decoding across the quantum low-density parity-check code landscape", Physical Review Research 2 4, 043423 (2020).
[23] Daniel Gottesman, "Opportunities and Challenges in Fault-Tolerant Quantum Computation", arXiv:2210.15844, (2022).
[24] Armanda O. Quintavalle, Michael Vasmer, Joschka Roffe, and Earl T. Campbell, "Single-Shot Error Correction of Three-Dimensional Homological Product Codes", PRX Quantum 2 2, 020340 (2021).
[25] Nicolas Delfosse, Michael E. Beverland, and Maxime A. Tremblay, "Bounds on stabilizer measurement circuits and obstructions to local implementations of quantum LDPC codes", arXiv:2109.14599, (2021).
[26] Ryan Babbush, Jarrod McClean, Michael Newman, Craig Gidney, Sergio Boixo, and Hartmut Neven, "Focus beyond quadratic speedups for error-corrected quantum advantage", arXiv:2011.04149, (2020).
[27] Oscar Higgott and Nikolas P. Breuckmann, "Improved Single-Shot Decoding of Higher-Dimensional Hypergraph-Product Codes", PRX Quantum 4 2, 020332 (2023).
[28] Armanda O. Quintavalle and Earl T. Campbell, "ReShape: a decoder for hypergraph product codes", arXiv:2105.02370, (2021).
[29] Nicolas Delfosse, Vivien Londe, and Michael Beverland, "Toward a Union-Find decoder for quantum LDPC codes", arXiv:2103.08049, (2021).
[30] Noah Berthusen and Daniel Gottesman, "Partial Syndrome Measurement for Hypergraph Product Codes", arXiv:2306.17122, (2023).
[31] Leonid P. Pryadko, "On maximum-likelihood decoding with circuit-level errors", Quantum 4, 304 (2020).
The above citations are from Crossref's cited-by service (last updated successfully 2024-05-12 15:36:39) and SAO/NASA ADS (last updated successfully 2024-05-12 15:36:40). The list may be incomplete as not all publishers provide suitable and complete citation data.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.